Let 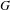$G$ be a semisimple Lie group of rank one and 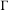$\unicode[STIX]{x1D6E4}$ be a torsion-free discrete subgroup of 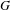$G$ . We show that in 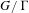$G/\unicode[STIX]{x1D6E4}$ , given 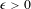$\unicode[STIX]{x1D716}>0$ , any trajectory of a unipotent flow remains in the set of points with injectivity radius larger than $\unicode[STIX]{x1D6FF}$ for a 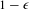$1-\unicode[STIX]{x1D716}$ proportion of the time, for some 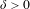$\unicode[STIX]{x1D6FF}>0$ . The result also holds for any finitely generated discrete subgroup 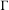$\unicode[STIX]{x1D6E4}$ and this generalizes Dani’s quantitative non-divergence theorem [On orbits of unipotent flows on homogeneous spaces. Ergod. Th. & Dynam. Sys.4(1) (1984), 25–34] for lattices of rank-one semisimple groups. Furthermore, for a fixed 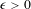$\unicode[STIX]{x1D716}>0$ , there exists an injectivity radius $\unicode[STIX]{x1D6FF}$ such that, for any unipotent trajectory 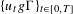$\{u_{t}g\unicode[STIX]{x1D6E4}\}_{t\in [0,T]}$ , either it spends at least a 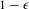$1-\unicode[STIX]{x1D716}$ proportion of the time in the set with injectivity radius larger than $\unicode[STIX]{x1D6FF}$ , for all large 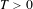$T>0$ , or there exists a 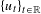$\{u_{t}\}_{t\in \mathbb{R}}$ -normalized abelian subgroup $L$ of 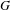$G$ which intersects 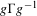$g\unicode[STIX]{x1D6E4}g^{-1}$ in a small covolume lattice. We also extend these results to when 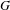$G$ is the product of rank-one semisimple groups and 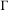$\unicode[STIX]{x1D6E4}$ a discrete subgroup of 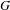$G$ whose projection onto each non-trivial factor is torsion free.