Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T05:00:33.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilsequences and multiple correlations along subsequences

Part of: Ergodic theory

Published online by Cambridge University Press:  08 October 2018

ANH NGOC LE
ANH NGOC LE*
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL 60208-2730, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The results of Bergelson, Host and Kra, and Leibman state that a multiple polynomial correlation sequence can be decomposed into a sum of a nilsequence (a sequence defined by evaluating a continuous function along an orbit in a nilsystem) and a null sequence (a sequence that goes to zero in density). We refine their results by proving that the null sequence goes to zero in density along polynomials evaluated at primes and along the Hardy sequence 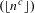$(\lfloor n^{c}\rfloor )$. In contrast, given a rigid sequence, we construct an example of a correlation whose null sequence does not go to zero in density along that rigid sequence. As a corollary of a lemma in the proof, the formula for the pointwise ergodic average along polynomials of primes in a nilsystem is also obtained.

Keywords

classical ergodic theorynumber theorymultiple correlationnilsequencenull sequence

MSC classification

Primary: 37A45: Relations with number theory and harmonic analysis
Secondary: 37A30: Ergodic theorems, spectral theory, Markov operators
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 6 , June 2020 , pp. 1634 - 1654
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. Rational ergodicity, bounded rational ergodicity and some continuous measures on the circle. Israel J. Math. 33(3) (1979), 181–197.Google Scholar
Austin, T.. Pleasant extensions retaining algebraic structure, I. J. Anal. Math. 125 (2015), 1–36.Google Scholar
Austin, T.. Pleasant extensions retaining algebraic structure, II. J. Anal. Math. 126 (2015), 1–111.Google Scholar
Badea, C. and Grivaux, S.. Kazhdan constants, continuous probability measures with large Fourier coefficients and rigidity sequences. Preprint, 2018, arXiv:1804.01369v1.Google Scholar
Bergelson, V., Del Junco, A., Lemańczyk, M. and Rosenblatt, J.. Rigidity and non-recurrence along sequences. Ergod. Th. & Dynam. Sys. 34(5) (2014), 1464–1502.Google Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303. With an appendix by Imre Ruzsa.Google Scholar
Cornfeld, I. P., Fomin, S. V. and Sinaĭ, Ya. G.. Ergodic Theory (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 245). Springer, New York, 1982. Translated from the Russian by A. B. Sosinskiĭ.Google Scholar
Donoso, S., Le, A. N., Moreira, J. and Sun, W.. Optimal lower bounds for multiple recurrence. Preprint, 2018, arXiv:1809.06912.Google Scholar
Eisner, T.. Nilsystems and ergodic averages along primes. Preprint, 2016, arXiv:1601.00562v3.Google Scholar
Eisner, T. and Grivaux, S.. Hilbertian Jamison sequences and rigid dynamical systems. J. Funct. Anal. 261 (2011), 2013–2052.Google Scholar
Fayad, B. and Thouvenot, J.. On the convergence to 0 of m n𝜉 mod 1. Acta Arith. 165 (2014), 327–332.Google Scholar
Frantzikinakis, N.. Multiple ergodic averages for three polynomials and applications. Trans. Amer. Math. Soc. 360(10) (2008), 5435–5475.Google Scholar
Frantzikinakis, N.. Equidistribution of spare sequences on nilmanifolds. J. Anal. Math. 109 (2009), 353–395.Google Scholar
Frantzikinakis, N.. Multiple recurrence and convergence for Hardy sequences of polynomial growth. J. Anal. Math. 112 (2010), 79–135.Google Scholar
Frantzikinakis, N.. Multiple correlation sequences and nilsequences. Invent. Math. 202(2) (2015), 875–892.Google Scholar
Frantzikinakis, N.. Some open problems on multiple ergodic averages. Bull. Hellenic Math. Soc. 60 (2016), 41–90.Google Scholar
Frantzikinakis, N., Host, B. and Kra, B.. Multiple recurrence and convergence for sequences related to the prime numbers. J. Reine Angew. Math. 611 (2007), 131–144.Google Scholar
Frantzikinakis, N., Host, B. and Kra, B.. The polynomial multidimensional Szemerédi theorem along shifted primes. Israel J. Math. 194(1) (2013), 331–348.Google Scholar
Green, B. and Tao, T.. Linear equations in primes. Ann. of Math. (2) 171(2) (2010), 1753–1850.Google Scholar
Green, B. and Tao, T.. The Mobius function is strongly orthogonal to nilsequences. Ann. of Math. (2) 175(2) (2012), 541–566.Google Scholar
Green, B., Tao, T. and Ziegler, T.. An inverse theorem for the Gowers U(s+1)[N]-norm. Ann. of Math. (2) 176(2) (2012), 1231–1372.Google Scholar
Host, B. and Kra, B.. Convergence of polynomial ergodic averages. Israel J. Math. 149 (2005), 1–19.Google Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161 (2005), 397–488.Google Scholar
Leibman, A.. Convergence of multiple ergodic averages along polynomials of several variables. Israel J. Math. 146 (2005), 303–315.Google Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial actions of Z d by translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25(1) (2005), 215–225.Google Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequences of translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 1 (2005), 201–213.Google Scholar
Leibman, A.. Multiple polynomial correlation sequences and nilsequences. Ergod. Th. & Dynam. Sys. 30 (2010), 841–854.Google Scholar
Leibman, A.. Nilsequences, null-sequences, and multiple correlation sequences. Ergod. Th. & Dynam. Sys. 35(1) (2015), 176–191. Corrected at https://people.math.osu.edu/leibman.1/preprints/msqx.pdf.Google Scholar
Moreira, J. and Richter, F.. A spectral refinement of the Bergelson–Host–Kra decomposition and multiple ergodic theorems. Ergod. Th. & Dynam. Sys. (2017), doi:10.1017/etds.2017.61. Published online 7 September 2017.Google Scholar
Tao, T. and Teräväinen, J.. The structure of logarithmically averaged correlations of multiplicative functions, with applications to the Chowla and Elliott conjectures. Preprint, 2017, arXiv:1708.02610.Google Scholar
Wooley, T. and Ziegler, T.. Multiple recurrence and convergence along the primes. Amer. J. Math. 134 (2012), 1705–1732.Google Scholar