Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-05T10:02:35.322Z Has data issue: false hasContentIssue false
  • English
  • Français

A new maximal inequality and its applications

Published online by Cambridge University Press:  19 September 2008

Joseph M. Rosenblatt  and
Mate Wierdl
Joseph M. Rosenblatt
Affiliation:
Department of Mathematics, The Ohio State University, 231 W. W. 18th Avenue, Columbus, OH. 43210, USA
Mate Wierdl
Affiliation:
Department of Mathematics, The Ohio State University, 231 W. W. 18th Avenue, Columbus, OH. 43210, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

There is a maximal inequality on the integers which implies not only the classical ergodic maximal inequality and certain maximal inequalities for moving averages and differentiation theory, but it also has the following consequence: let P1 ≤ P2 ≤ … ≤ Pk+1 be positive integers. For a σ-finite measure-preserving system (Ω, β, μ, T) and an a.e. finite β-measurable f denote

Then for any λ > 0 and f ∈ L1(Ω)

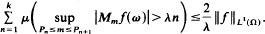
We show how the multi-parametric and superadditive versions of the previous equation can be obtained from the corresponding inequality for reversed supermartingales. The possibility of similar theorems for martingales and other sequences is also discussed.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 12 , Issue 3 , September 1992 , pp. 509 - 558
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A-Ja]Akcoglu, M. & del Junco, A.. Convergence of averages of point transformations. Proc Amer. Math. Soc. 49 (1975), 265–266.Google Scholar
[B-J-R]Bellow, A., Jones, R. & Rosenblatt, J.. Convergence of moving averages. Ergod. Th. & Dynam. Sys. 10 (1990), 43–62.CrossRefGoogle Scholar
[Ba-K]Baum, L. & Katz, M.. Convergence rates in the law of large numbers. Trans. Amer. Math. Soc. 120 (1965), 108–123.CrossRefGoogle Scholar
[C]Calderon, A.. Ergodic theory and translation invariant operators. Proc. Nat. Acad. Sci. USA 59 (1968), 349–353.Google Scholar
[Jo-Z]Johnson, W. & Zinn, J.. Private communication.Google Scholar
[Ju-R]del Junco, A. & Rosenblatt, J.. Counterexamples in ergodic theory and number theory. Math. Ann. 245 (1979), 185–197.CrossRefGoogle Scholar
[K]Katz, M.. The probability in the tail of a distribution. Ann. Math. Statist. 34 (1963), 312–318.Google Scholar
[Kak-Y]Kakutani, S. & Yosida, K.. Birkhofi's ergodic theorem and the maximal ergodic theorem. Proc. Imp. Akad. Tokyo 15 (1939), 165–168.Google Scholar
[Kr]Krengel, U.. Ergodic Theorems. Vol. 6. de Gruyter, Berlin, 1985.CrossRefGoogle Scholar
[N-S]Nagel, A. & Stein, E.. On certain maximal functions and approach regions. Adv. Math. 54 (1984), 83–106.Google Scholar
[Sa]Sawyer, S.. Maximal inequalities of weak type. Ann. Math. 84 (1966), 157–174.Google Scholar