Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T09:31:33.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Multifractal analysis for projections of Gibbs and related measures

Published online by Cambridge University Press:  26 May 2010

JULIEN BARRAL  and
IMEN BHOURI
JULIEN BARRAL
Affiliation:
LAGA (UMR 7539), Institut Galilée, 99 av. Jean-Baptiste Clément, 93430 Villetaneuse, France (email: [email protected])
IMEN BHOURI
Affiliation:
Département de Mathématiques, Faculté des Sciences de Monastir, 5019 Monastir, Tunisia (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let n>m≥1 be two integers. At first we obtain general results for the multifractal analysis of the orthogonal projections on m-dimensional linear subspaces of singular measures μ on ℝn satisfying the multifractal formalism. The results hold for γn,m-almost every such subspace, where γn,m is the uniform measure on the Grassmannian manifold Gn,m. Let μ be such a measure and suppose that its upper Hausdorff dimension is less than or equal to m. Let I stand for the interval over which the singularity spectrum of μ is increasing. We prove that there exists a non-trivial subinterval 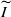of I such that for every 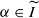, for γn,m-almost every m-dimensional subspace V, the multifractal formalism holds at α for μV, the orthogonal projection of μ on V. Moreover, in some cases the result is optimal in the sense that the interval 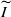is maximal in I. Also, we determine the Lq-spectrum τμV(q) on the minimal interval J necessary to recover the singularity spectrum of μV over 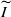as the Legendre transform of τμV. The interval J and the function τμV(q) do not depend on V, and τμV(q) can differ from τμ on a non-trivial interval. For Gibbs measures and some of their discrete counterparts, we show the stronger uniform result: for γn,m-almost every m-dimensional subspace V, the multifractal formalism holds for μV over the whole interval 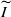. As an application, we obtain a part of the singularity spectrum of some self-similar measures on attractors of iterated function systems which do not satisfy the weak separation condition.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 3 , June 2011 , pp. 673 - 701
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Arbeiter, M. and Patszchke, N.. Random self-similar multifractals. Math. Nachr. 181 (1996), 5–42.CrossRefGoogle Scholar
[2]Bahroun, F. and Bhouri, I.. Multifractals and projections. Extracta Math. 21 (2006), 83–91.Google Scholar
[3]Barral, J.. Continuity of the multifractal spectrum of a random statistically self-similar measure. J. Theor. Probab. 13 (2000), 1027–1060.CrossRefGoogle Scholar
[4]Barral, J. and Seuret, S.. Combining multifractal additive and multiplicative chaos. Commun. Math. Phys. 257(2) (2005), 473–497.CrossRefGoogle Scholar
[5]Barral, J. and Seuret, S.. Heterogeneous ubiquitous systems in ℝd and Hausdorff dimension. Bull. Braz. Math. Soc. 38 (2007), 476–515.CrossRefGoogle Scholar
[6]Barral, J. and Seuret, S.. The multifractal nature of heterogeneous sums of Dirac masses. Math. Proc. Camb. Philos. Soc. 144 (2008), 707–727.CrossRefGoogle Scholar
[7]Barral, J. and Seuret, S.. The singularity spectrum of the inverse of cookie-cutters. Ergod. Th. & Dynam. Sys. 29 (2009), 1075–1095.CrossRefGoogle Scholar
[8]Barreira, L., Pesin, Y. and Schmeling, J.. Multifractal spectra and multifractal rigidity for horseshoes. J. Dynam. Control Syst. 3 (1997), 33–49.CrossRefGoogle Scholar
[9]Barreira, L. and Valls, C.. Multifractal structure of two-dimensional horseshoes. Commun. Math. Phys. 266 (2006), 455–470.CrossRefGoogle Scholar
[10]Ben Nasr, F.. Analyse multifractale de mesures. C. R. Acad. Sci. Paris Sér. I 319 (1994), 807–810.Google Scholar
[11]Ben Nasr, F., Bhouri, I. and Heurteaux, Y.. The validity of the multifractal formalism: results and examples. Adv. Math. 165 (2002), 264–284.CrossRefGoogle Scholar
[12]Bhouri, I.. Une condition de validité du formalisme multifractal pour les mesures. PhD Thesis, Faculté des Sciences de Monastir, 1999.Google Scholar
[13]Brown, G., Michon, G. and Peyrière, J.. On the multifractal analysis of measures. J. Statist. Phys. 66 (1992), 775–790.CrossRefGoogle Scholar
[14]Cawley, R. and Mauldin, R. D.. Multifractal decompositions of Moran fractals. Adv. Math. 92 (1992), 196–236.CrossRefGoogle Scholar
[15]Dodson, M. M., Melián, M. V., Pestane, D. and Vélani, S. L.. Patterson measure and ubiquity. Ann. Acad. Sci. Fenn. Ser. A I Math. 20(1) (1995), 37–60.Google Scholar
[16]Edgar, G. A. and Mauldin, R. D.. Multifractal decompositions of digraph recursive fractals. Proc. Lond. Math. Soc. 65 (1992), 604–628.CrossRefGoogle Scholar
[17]Falconer, K. J.. Fractal Geometry. Mathematical Foundations and Applications. John Wiley, Chichester, 1990.Google Scholar
[18]Falconer, K. J.. The multifractal spectrum of statistically self-similar measures. J. Theor. Probab. 7 (1994), 681–702.CrossRefGoogle Scholar
[19]Falconer, K. J.. Representation of families of sets by measures, dimension spectra and Diophantine approximation. Math. Proc. Camb. Philos. Soc. 128 (2000), 111–121.CrossRefGoogle Scholar
[20]Falconer, K. J. and O’Neil, T.. Convolutions and the geometry of multifractal measures. Math. Nachr. 204 (1999), 61–82.CrossRefGoogle Scholar
[21]Fan, A.-H.. Sur la dimension des mesures. Studia Math. 111 (1994), 1–17.CrossRefGoogle Scholar
[22]Fan, A.-H. and Lau, K. S.. Iterated function systems and Ruelle operators. J. Math. Anal. Appl. 231 (1999), 319–344.CrossRefGoogle Scholar
[23]Feng, D.-J.. The limit Rademacher functions and Bernoulli convolutions associated with Pisot numbers. Adv. Math. 195 (2005), 24–101.CrossRefGoogle Scholar
[24]Feng, D.-J.. Gibbs properties of self-conformal measures and the multifractal formalism. Ergod. Th. & Dynam. Sys. 27 (2007), 787–812.CrossRefGoogle Scholar
[25]Feng, D.-J.. Lyapunov exponents for products of matrices and multifractal analysis. Part II: general matrices. Israel J. Math. 170 (2009), 355–394.CrossRefGoogle Scholar
[26]Feng, D.-J. and Lau, K. S.. Multifractal formalism for self-similar measures with weak separation condition. J. Math. Pures Appl. 92 (2009), 407–428.CrossRefGoogle Scholar
[27]Feng, D.-J., Lau, K. S. and Wang, X.-Y.. Some exceptional phenomena in multifractal formalism. II. Asian J. Math. 9 (2005), 473–488.CrossRefGoogle Scholar
[28]Feng, D.-J. and Olivier, E.. Multifractal analysis of the weak Gibbs measures and phase transition – application to some Bernoulli convolutions. Ergod. Th. & Dynam. Sys. 23 (2003), 1751–1784.CrossRefGoogle Scholar
[29]Frisch, U. and Parisi, G.. Fully developed turbulence and intermittency in turbulence, and predictability in geophysical fluid dynamics and climate dynamics. International School of Physics ‘Enrico Fermi’, Course 88. Ed. Ghil, M.. North-Holland, Amsterdam, 1985, pp. 84–88.Google Scholar
[30]Halsey, T. C., Jensen, M. H., Kadanoff, L. P., Procaccia, I. and Shraiman, B. I.. Fractal measures and their singularities: the characterisation of strange sets. Phys. Rev. A 33 (1986), 1141–1151.CrossRefGoogle ScholarPubMed
[31]Hentschel, H. G. and Procaccia, I.. The infinite number of generalized dimensions of fractals and strange attractors. Physica 8D (1983), 435–444.Google Scholar
[32]Holley, R. and Waymire, E. C.. Multifractal dimensions and scaling exponents for strongly bounded random fractals. Ann. Appl. Probab. 2 (1992), 819–845.CrossRefGoogle Scholar
[33]Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.CrossRefGoogle Scholar
[34]Hu, X. and Taylor, S. J.. Fractal properties of products and projections of measures in ℝd. Math. Proc. Camb. Philos. Soc. 115 (1994), 527–544.CrossRefGoogle Scholar
[35]Hunt, B. R. and Kaloshin, V. Y.. How projections affect the dimension spectrum of fractal measures. Nonlinearity 10 (1997), 1031–1046.CrossRefGoogle Scholar
[36]Jaffard, S.. Old friends revisited: the multifractal nature of some classical functions. J. Fourier Anal. Appl. 3(1) (1997), 1–22.CrossRefGoogle Scholar
[37]Jaffard, S.. On lacunary wavelet series. Ann. Appl. Probab. 10(1) (2000), 313–329.CrossRefGoogle Scholar
[38]Lau, K. S. and Ngai, S.-M.. Multifractal measures and a weak separation condition. Adv. Math. 141 (1999), 45–96.CrossRefGoogle Scholar
[39]Lau, K. S. and Wang, X.-Y.. Some exceptional phenomena in multifractal formalism I. Asian J. Math. 9 (2005), 275–294.CrossRefGoogle Scholar
[40]Mastrand, J. M.. Some fundamental geometrical properties of plane sets of fractional dimensions. Proc. Lond. Math. Soc. 4(3) (1954), 257–302.CrossRefGoogle Scholar
[41]Mattila, P.. Hausdorff dimension, orthogonal projections and intersections with planes. Ann. Acad. Sci. Fenn. Ser. A I Math. 1(2) (1975), 227–244.CrossRefGoogle Scholar
[42]Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces, Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics, 44). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[43]Ngai, S. M.. A dimension result arising from the L q-spectrum of a measure. Proc. Amer. Math. Soc. 125 (1997), 2943–2951.CrossRefGoogle Scholar
[44]Olsen, L.. Random geometrically graph directed self-similar multifractals. Pitman Res. Notes Math. Ser. 307 (1994).Google Scholar
[45]Olsen, L.. A multifractal formalism. Adv. Math. 116 (1995), 82–196.CrossRefGoogle Scholar
[46]Olsen, L. and Snigireva, N.. Multifractal spectra of in-homogenous self-similar measures. Indiana Univ. Math. J. 57 (2008), 1789–1843.CrossRefGoogle Scholar
[47]O’Neil, T.. The multifractal spectrum of projected measures in Euclidean spaces. Chaos Solitons Fractals 11 (2000), 901–921.CrossRefGoogle Scholar
[48]Palis, J.. Homoclinic orbits, hyperbolic dynamics and dimension of Cantor sets. The Lefschetz Centennial Conference, Part III, Mexico City, 1984 (Contemporary Mathematics, 58). American Mathematical Society, Providence, RI, 1987, pp. 203–216.Google Scholar
[49]Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque (1990), 187–188.Google Scholar
[50]Patzschke, N.. Self-conformal multifractal measures. Adv. Appl. Math. 19 (1997), 486–513.CrossRefGoogle Scholar
[51]Peres, Y., Rams, M., Simon, K. and Solomyak, B.. Equivalence of positive Hausdorff measure and the open set condition for self-conformal sets. Proc. Amer. Math. Soc. 129 (2001), 2689–2699.CrossRefGoogle Scholar
[52]Pesin, Y.. Dimension Theory in Dynamical Systems: Contemporary Views and Applications (Chicago Lectures in Mathematics). The University of Chicago Press, Chicago, IL, 1997.CrossRefGoogle Scholar
[53]Pesin, Y. and Weiss, H.. A multifractal analysis of equilibrium measures for conformal expanding maps and Moran-like geometric constructions. J. Statist. Phys. 86 (1997), 233–275.CrossRefGoogle Scholar
[54]Pesin, Y. and Weiss, H.. The multifractal analysis of Gibbs measures: motivation, mathematical foundation, and examples. Chaos 7 (1997), 89–106.CrossRefGoogle ScholarPubMed
[55]Rand, D. A.. The singularity spectrum f(α) for cookie-cutters. Ergod. Th. & Dynam. Sys. 9 (1989), 527–541.CrossRefGoogle Scholar
[56]Riedi, R. H.. An improved multifractal formalism and self-similar measures. J. Math. Anal. Appl. 189 (1995), 462–490.CrossRefGoogle Scholar
[57]Schief, A.. Separation properties for self-similar sets. Proc. Amer. Math. Soc. 122 (1994), 111–115.CrossRefGoogle Scholar
[58]Shmerkin, P.. A modified multifractal formalism for a class of self-similar measures with overlap. Asian J. Math. 9 (2005), 323–348.CrossRefGoogle Scholar
[59]Testud, B.. Mesures quasi-Bernoulli au sens faible: résultats et exemples. Ann. Inst. Poincaré Probab. Statist. 42 (2006), 1–35.CrossRefGoogle Scholar
[60]Testud, B.. Phase transitions for the multifractal analysis of self-similar measures. Nonlinearity 19 (2006), 1201–1217.CrossRefGoogle Scholar