Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-07T11:23:09.526Z Has data issue: false hasContentIssue false
  • English
  • Français

Möbius disjointness along ergodic sequences for uniquely ergodic actions

Published online by Cambridge University Press:  13 March 2018

JOANNA KUŁAGA-PRZYMUS  and
MARIUSZ LEMAŃCZYK
JOANNA KUŁAGA-PRZYMUS
Affiliation:
Institute of Mathematics, Polish Acadamy of Sciences, Śniadeckich 8, 00-956 Warszawa, Poland Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland email [email protected], [email protected]
MARIUSZ LEMAŃCZYK
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

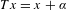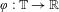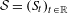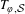We show that there is an irrational rotation $Tx=x+\unicode[STIX]{x1D6FC}$ on the circle $\mathbb{T}$ and a continuous $\unicode[STIX]{x1D711}:\mathbb{T}\rightarrow \mathbb{R}$ such that for each (continuous) uniquely ergodic flow ${\mathcal{S}}=(S_{t})_{t\in \mathbb{R}}$ acting on a compact metric space $Y$, the automorphism $T_{\unicode[STIX]{x1D711},{\mathcal{S}}}$ acting on 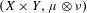$(X\times Y,\unicode[STIX]{x1D707}\otimes \unicode[STIX]{x1D708})$ by the formula 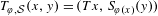$T_{\unicode[STIX]{x1D711},{\mathcal{S}}}(x,y)=(Tx,S_{\unicode[STIX]{x1D711}(x)}(y))$, where $\unicode[STIX]{x1D707}$ stands for the Lebesgue measure on $\mathbb{T}$ and $\unicode[STIX]{x1D708}$ denotes the unique 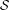${\mathcal{S}}$-invariant measure, has the property of asymptotically orthogonal powers. This gives a class of relatively weakly mixing extensions of irrational rotations for which Sarnak’s conjecture on the Möbius disjointness holds for all uniquely ergodic models of 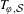$T_{\unicode[STIX]{x1D711},{\mathcal{S}}}$. Moreover, we obtain a class of ‘random’ ergodic sequences 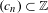$(c_{n})\subset \mathbb{Z}$ such that if 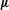$\boldsymbol{\unicode[STIX]{x1D707}}$ denotes the Möbius function, then

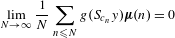$$\begin{eqnarray}\lim _{N\rightarrow \infty }\frac{1}{N}\mathop{\sum }_{n\leq N}g(S_{c_{n}}y)\boldsymbol{\unicode[STIX]{x1D707}}(n)=0\end{eqnarray}$$
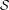for all (continuous) uniquely ergodic flows ${\mathcal{S}}$, all $g\in C(Y)$ and 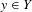$y\in Y$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 10 , October 2019 , pp. 2793 - 2826
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50) . American Mathematical Society, Providence, RI, 1997.Google Scholar
Aaronson, J., Lemańczyk, M., Mauduit, C. and Nakada, H.. Koksma inequality and group extensions of Kronecker transformations. Algorithms, Fractals and Dynamics. Ed. Takahashi, Y.. Plenum, New York, 1995, pp. 27–50.Google Scholar
El Abdalaoui, E. H., Kasjan, S. and Lemańczyk, M.. 0–1 sequences of the Thue–Morse type and Sarnak’s conjecture. Proc. Amer. Math. Soc. 144 (2016), 161–176.Google Scholar
El Abdalaoui, E. H., Kułaga-Przymus, J., Lemańczyk, M. and de la Rue, T.. The Chowla and the Sarnak conjectures from ergodic theory point of view. Discrete Contin. Dyn. Syst. 37 (2017), 2899–2944.Google Scholar
El Abdalaoui, E. H., Kułaga-Przymus, J., Lemańczyk, M. and de la Rue, T.. Möbius disjointness for models of an ergodic system and beyond. Israel J. Math., to appear, Preprint, 2017, arXiv:1704.03506.Google Scholar
El Abdalaoui, E. H., Lemańczyk, M. and de la Rue, T.. Asymptotic orthogonality of powers for quasi-discrete spectrum automorphisms. Int. Math. Res. Not. IMRN 14 (2017), 4350–4368.Google Scholar
Abramov, L. M.. Metric automorphisms with quasi-discrete spectrum. Izv. Akad. Nauk SSSR Ser. Mat. 26 (1962), 513–530.Google Scholar
Arnoux, P.. Sturmian sequences. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794) . Springer, Berlin, 2002, pp. 143–198.Google Scholar
Bergelson, V., Boshernitzan, M. and Bourgain, J.. Some results on nonlinear recurrence. J. Anal. Math. 62 (1994), 29–46.Google Scholar
Boshernitzan, M. and Wierdl, M.. Ergodic theorems along sequences and Hardy fields. Proc. Natl. Acad. Sci. USA 93 (1996), 8205–8207.Google Scholar
Bourgain, J., Sarnak, P. and Ziegler, T.. Disjointness of Möbius from horocycle flows. From Fourier Analysis and Number Theory to Radon Transforms and Geometry (Developments in Mathematics, 28) . Springer, New York, 2013, pp. 67–83.Google Scholar
Conze, J.-P. and Piȩkniewska, A.. On multiple ergodicity of affine cocycles over irrational rotations. Israel J. Math. 201 (2014), 543–584.Google Scholar
Cornfeld, I. P., Fomin, S. V. and Sinaĭ, Y. G.. Ergodic Theory (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 245) . Springer, New York, 1982.Google Scholar
Danilenko, A. I.. Entropy theory from the orbital point of view. Monatsh. Math. 134(2) (2001), 121–141.Google Scholar
Danilenko, A. I. and Lemańczyk, M.. A class of multipliers for 𝓦⊥ . Israel J. Math. 148 (2005), 137–168. Probability in mathematics.Google Scholar
Deshouillers, J.-M., Drmota, M. and Müllner, C.. Automatic sequences generated by synchronizing automata fulfill the Sarnak conjecture. Studia Math. 231 (2015), 83–95.Google Scholar
Downarowicz, T. and Kasjan, S. A.. Odometers and Toeplitz systems revisited in the context of Sarnak’s conjecture. Studia Math. 229 (2015), 45–72.Google Scholar
Ferenczi, S., Kułaga-Przymus, J., Lemańczyk, M. and Mauduit, C.. Substitutions and Möbius disjointness. Ergodic Theory, Dynamical Systems, and the Continuing Influence of John C. Oxtoby (Contemporary in Mathematics, 678) . American Mathematical Society, Providence, RI, 2016, pp. 151–173.Google Scholar
Flaminio, L., Frączek, K., Kułaga-Przymus, J. and Lemańczyk, M.. Approximate orthogonality of powers for ergodic affine unipotent diffeomorphisms on nilmanifolds. Studia Math., to appear, 2016, arXiv:1609.00699.Google Scholar
Frączek, K., Lemańczyk, M. and Lesigne, E.. Mild mixing property for special flows under piecewise constant functions. Discrete Contin. Dyn. Syst. 19 (2007), 691–710.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981, M. B. Porter Lectures.Google Scholar
Glasner, E.. Ergodic Theory Via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Green, B. and Tao, T.. The Möbius function is strongly orthogonal to nilsequences. Ann. of Math. (2) 175 (2012), 541–566.Google Scholar
Karagulyan, D.. On Möbius orthogonality for subshifts of finite type with positive topological entropy. Studia Math. 237 (2017), 277–282.Google Scholar
Kátai, I.. A remark on a theorem of H. Daboussi. Acta Math. Hungar. 47 (1986), 223–225.Google Scholar
Kułaga-Przymus, J. and Lemańczyk, M.. The Möbius function and continuous extensions of rotations. Monatsh. Math. 178 (2015), 553–582.Google Scholar
Kwiatkowski, J., Lemańczyk, M. and Rudolph, D.. A class of real cocycles having an analytic coboundary modification. Israel J. Math. 87 (1994), 337–360.Google Scholar
Lehrer, E.. Topological mixing and uniquely ergodic systems. Israel J. Math. 57 (1987), 239–255.Google Scholar
Lemańczyk, M. and Lesigne, E.. Ergodicity of Rokhlin cocycles. J. Anal. Math. 85 (2001), 43–86.Google Scholar
Lemańczyk, M., Lesigne, E., Parreau, F., Volný, D. and Wierdl, M.. Random ergodic theorems and real cocycles. Israel J. Math. 130 (2002), 285–321.Google Scholar
Lemańczyk, M., Mentzen, M. K. and Nakada, H.. Semisimple extensions of irrational rotations. Studia Math. 156 (2003), 31–57.Google Scholar
Lemańczyk, M. and Parreau, F.. Rokhlin extensions and lifting disjointness. Ergod. Th. & Dynam. Sys. 23 (2003), 1525–1550.Google Scholar
Lemańczyk, M. and Parreau, F.. Lifting mixing properties by Rokhlin cocycles. Ergod. Th. & Dynam. Sys. 32 (2012), 763–784.Google Scholar
Lemańczyk, M., Parreau, F. and Volný, D.. Ergodic properties of real cocycles and pseudo-homogeneous Banach spaces. Trans. Amer. Math. Soc. 348 (1996), 4919–4938.Google Scholar
Lesigne, E.. On the sequence of integer parts of a good sequence for the ergodic theorem. Comment. Math. Univ. Carolin. 36 (1995), 737–743.Google Scholar
Liu, J. and Sarnak, P.. The Möbius function and distal flows. Duke Math. J. 164 (2015), 1353–1399.Google Scholar
Matomäki, K. and Radziwiłł, M.. Multiplicative functions in short intervals. Ann. of Math. (2) 183 (2016), 1015–1056.Google Scholar
Peckner, R.. Two dynamical perspectives on the randomness of the Mobius function. PhD Thesis, ProQuest LLC, Princeton University, Ann Arbor, MI, 2015.Google Scholar
Sarnak, P.. Three lectures on the Möbius function, randomness and dynamics. http://publications.ias.edu/sarnak/.Google Scholar
Schmidt, K.. Cocycles on Ergodic Transformation Groups (Macmillan Lectures in Mathematics, 1) . Macmillan Company of India, Ltd., Delhi, 1977.Google Scholar
Wang, Z.. Möbius disjointness for analytic skew products. Invent. Math. 209(1) (2017), 175–196.Google Scholar