Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T03:21:42.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Measure-theoretic chaos

Published online by Cambridge University Press:  31 August 2012

TOMASZ DOWNAROWICZ  and
YVES LACROIX
TOMASZ DOWNAROWICZ
Affiliation:
Institute of Mathematics and Computer Science, Wrocław University of Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland (email: [email protected])
YVES LACROIX
Affiliation:
Institut des Sciences de l’Ingénieur de Toulon et du Var, Avenue G. Pompidou, B.P. 56, 83162 La Valette du Var Cedex, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We define new isomorphism invariants for ergodic measure-preserving systems on standard probability spaces, called measure-theoretic chaos and measure-theoretic$^+$ chaos. These notions are analogs of the topological chaos DC2 and its slightly stronger version (which we denote by 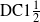$\text {DC}1\frac 12$). We prove that: (1) if a topological system is measure-theoretically (measure-theoretically$^+$) chaotic with respect to at least one of its ergodic measures then it is topologically DC2 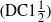$(\text {DC}1\frac 12)$ chaotic; (2) every ergodic system with positive Kolmogorov–Sinai entropy is measure-theoretically$^+$ chaotic (even in a slightly stronger uniform sense). We provide an example showing that the latter statement cannot be reversed, that is, of a system of entropy zero with uniform measure-theoretic$^+$chaos.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 1 , February 2014 , pp. 110 - 131
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[BSS]Balibrea, F., Smítal, J. and Štefánková, M.. The three versions of distributional chaos. Chaos Solitons Fractals 23 (2005), 1581–1583.Google Scholar
[BGKM]Blanchard, F., Glasner, E., Kolyada, S. and Maass, A.. On Li–Yorke pairs. J. Reine Angew. Math. 547 (2002), 51–68.Google Scholar
[D]Downarowicz, T.. Positive topological entropy implies chaos DC2. Proc. Amer. Math. Soc. (2011) to appear, arXiv:1110.5201v1 [math.DS].Google Scholar
[DL1]Downarowicz, T. and Lacroix, Y.. Topological entropy zero and asymptotic pairs. Israel J. Math. 189 (2012), 323–336.Google Scholar
[DL2]Downarowicz, T. and Lacroix, Y.. Forward mean proximal pairs and zero entropy. Israel J. Math. xxx (2012), doi:10.1007/s11856-012-0016-1.Google Scholar
[LY]Li, T. Y. and Yorke, J. A.. Period three implies chaos. Amer. Math. Monthly 82 (1975), 985–992.Google Scholar
[OW]Ornstein, D. and Weiss, B.. Mean distality and tightness. Proc. Steklov Inst. Math. 244 (2004), 312–319.Google Scholar
[P]Pikuła, R.. On some notions of chaos in dimension zero. Colloq. Math. 107 (2007), 167–177.Google Scholar
[SS]Schweizer, B. and Smítal, J.. Measures of chaos and a spectral decomposition of dynamical systems on the interval. Trans. Amer. Math. Soc. 344 (1994), 737–754.Google Scholar
[Se]Serafin, J.. Non-existence of a universal zero entropy system. Israel J. Math. xxx (2012), 1–10, doi:10.1007/s11856-011-0219-x.Google Scholar
[SSt]Smítal, J. and Štefánková, M.. Distributional chaos for triangular maps. Chaos Solitons Fractals 21 (2004), 1125–1128.Google Scholar
[WW]Wu, H. and Wang, H.. Measure-theoretical everywhere chaos and equicontinuity via Furstenberg families. Int. J. Contemp. Math. Sci. 5 (2010), 1373–1384.Google Scholar