No CrossRef data available.
Published online by Cambridge University Press: 17 March 2023
For a 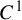 $C^1$ non-conformal repeller, this paper proves that there exists an ergodic measure of full Carathéodory singular dimension. For an average conformal hyperbolic set of a
$C^1$ non-conformal repeller, this paper proves that there exists an ergodic measure of full Carathéodory singular dimension. For an average conformal hyperbolic set of a 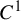 $C^1$ diffeomorphism, this paper constructs a Borel probability measure (with support strictly inside the repeller) of full Hausdorff dimension. If the average conformal hyperbolic set is of a
$C^1$ diffeomorphism, this paper constructs a Borel probability measure (with support strictly inside the repeller) of full Hausdorff dimension. If the average conformal hyperbolic set is of a 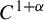 $C^{1+\alpha }$ diffeomorphism, this paper shows that there exists an ergodic measure of maximal dimension.
$C^{1+\alpha }$ diffeomorphism, this paper shows that there exists an ergodic measure of maximal dimension.