Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:44:32.052Z Has data issue: false hasContentIssue false
  • English
  • Français

Measure preserving actions of affine semigroups and 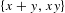$\{x+y,xy\}$ patterns

Published online by Cambridge University Press:  26 July 2016

VITALY BERGELSON  and
JOEL MOREIRA
VITALY BERGELSON
Affiliation:
Department of Mathematics, The Ohio State University, Math Building, 231 West 18th Avenue, Columbus, OH 43201, USA email [email protected], [email protected]
JOEL MOREIRA
Affiliation:
Department of Mathematics, The Ohio State University, Math Building, 231 West 18th Avenue, Columbus, OH 43201, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Ergodic and combinatorial results obtained in Bergelson and Moreira [Ergodic theorem involving additive and multiplicative groups of a field and 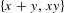$\{x+y,xy\}$ patterns. Ergod. Th. & Dynam. Sys. to appear, published online 6 October 2015, doi:10.1017/etds.2015.68], involved measure preserving actions of the affine group of a countable field 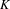$K$. In this paper, we develop a new approach, based on ultrafilter limits, which allows one to refine and extend the results obtained in Bergelson and Moreira, op. cit., to a more general situation involving measure preserving actions of the non-amenable affine semigroups of a large class of integral domains. (The results and methods in Bergelson and Moreira, op. cit., heavily depend on the amenability of the affine group of a field.) Among other things, we obtain, as a corollary of an ultrafilter ergodic theorem, the following result. Let 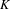$K$ be a number field and let 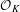${\mathcal{O}}_{K}$ be the ring of integers of 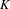$K$. For any finite partition 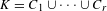$K=C_{1}\cup \cdots \cup C_{r}$, there exists 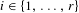$i\in \{1,\ldots ,r\}$ such that, for many 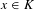$x\in K$ and many 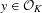$y\in {\mathcal{O}}_{K}$, 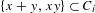$\{x+y,xy\}\subset C_{i}$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 2 , April 2018 , pp. 473 - 498
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V.. Ergodic Ramsey theory–an update. Ergodic Theory of Z d Actions (London Mathematical Society Lecture Note Series, 228) . Cambridge University Press, Cambridge, 1996, pp. 1–61.Google Scholar
Bergelson, V.. The multifarious Poincaré recurrence theorem. Descriptive Set Theory and Dynamical Systems (London Mathematical Society Lecture Note Series, 277) . Cambridge University Press, Cambridge, 2000, pp. 31–57.CrossRefGoogle Scholar
Bergelson, V.. Minimal idempotents and ergodic Ramsey theory. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310) . Cambridge University Press, Cambridge, 2003, pp. 8–39.CrossRefGoogle Scholar
Bergelson, V.. Ultrafilters, IP sets, dynamics, and combinatorial number theory. Ultrafilters Across Mathematics (Contemporary Mathematics, 530) . American Mathematical Society, Providence, RI, 2010, pp. 23–47.CrossRefGoogle Scholar
Bergelson, V., Furstenberg, H. and McCutcheon, R.. IP-sets and polynomial recurrence. Ergod. Th. & Dynam. Sys. 16(5) (1996), 963–974.CrossRefGoogle Scholar
Bergelson, V. and Hindman, N.. Nonmetrizable topological dynamics and Ramsey theory. Trans. Amer. Math. Soc. 320(1) (1990), 293–320.CrossRefGoogle Scholar
Bergelson, V. and Hindman, N.. On IP∗ sets and central sets. Combinatorica 14(3) (1994), 269–277.CrossRefGoogle Scholar
Bergelson, V., Johnson, J. and Moreira, J.. New polynomial and multidimensional extensions of classical partition results. Submitted. Preprint, 2015, arXiv:1501.02408.Google Scholar
Bergelson, V. and McCutcheon, R.. Central sets and a non-commutative Roth theorem. Amer. J. Math. 129(5) (2007), 1251–1275.CrossRefGoogle Scholar
Bergelson, V. and Moreira, J.. Ergodic theorem involving additive and multiplicative groups of a field and $\{x+y,xy\}$ patterns. Ergod. Th. & Dynam. Sys. to appear, published online 6 October 2015, doi:10.1017/etds.2015.68.CrossRefGoogle Scholar
Bergelson, V. and Robertson, D.. Polynomial recurrence with large intersection over countable fields. Israel J. Math. to appear. Preprint, 2014, arXiv:1409.6774.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
Green, B. and Sanders, T.. Monochromatic sums and products. Discrete Analysis 2016, article 5, pp. 1–43.CrossRefGoogle Scholar
Hindman, N. and Strauss, D.. Algebra in the Stone–Čech Compactification. Walter de Gruyter & Co., Berlin, 1998.CrossRefGoogle Scholar
Schur, I.. Über die kongruenz x m + y m ≡ z m (mod p). Jahresber. Dtsch. Math.-Ver. 25 (1916), 114–117.Google Scholar