Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:05:43.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Marked boundary rigidity for surfaces

Published online by Cambridge University Press:  08 November 2016

COLIN GUILLARMOU  and
MARCO MAZZUCCHELLI Open the ORCID record for MARCO MAZZUCCHELLI [Opens in a new window]
COLIN GUILLARMOU
Affiliation:
DMA, UMR 8553 CNRS, École Normale Supérieure, 45 rue d’Ulm, 75230 Paris Cedex 05, France email [email protected]
MARCO MAZZUCCHELLI
Affiliation:
UMPA, UMR 5669 CNRS, École Normale Supérieure de Lyon, 46 allée d’Italie, 69364 Lyon Cedex 07, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that, on an oriented compact surface, two sufficiently 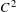$C^{2}$-close Riemannian metrics with strictly convex boundary, no conjugate points, hyperbolic trapped set for their geodesic flows and the same marked boundary distance are isometric via a diffeomorphism that fixes the boundary. We also prove that the same conclusion holds on a compact surface for any two negatively curved Riemannian metrics with strictly convex boundary and the same marked boundary distance, extending a result of Croke and Otal.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 4 , June 2018 , pp. 1459 - 1478
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Croke, C. B., Fathi, A. and Feldman, J.. The marked length-spectrum of a surface of nonpositive curvature. Topology 31(4) (1992), 847–855.CrossRefGoogle Scholar
Croke, C. B. and Herreros, P.. Lens rigidity with trapped geodesics in two dimensions. Asian J. Math. 20(1) (2016), 47–57.CrossRefGoogle Scholar
Croke, C. B.. Rigidity for surfaces of nonpositive curvature. Comment. Math. Helv. 65(1) (1990), 150–169.CrossRefGoogle Scholar
Croke, C. B.. Rigidity and the distance between boundary points. J. Differential Geom. 33(2) (1991), 445–464.CrossRefGoogle Scholar
Dyatlov, S. and Guillarmou, C.. Microlocal limits of plane waves and Eisenstein functions. Ann. Sci. Éc. Norm. Supér. (4) 47(2) (2014), 371–448.CrossRefGoogle Scholar
Dyatlov, S. and Guillarmou, C.. Pollicott–Ruelle resonances for open systems. Ann. Henri Poincaré (2016) to appear, Preprint arXiv:1410.5516.Google Scholar
Earle, C. J. and Schatz, A.. Teichmüller theory for surfaces with boundary. J. Differential Geom. 4 (1970), 169–185.CrossRefGoogle Scholar
Gromoll, D., Klingenberg, W. and Meyer, W.. Riemannsche Geometrie im Großen (Lecture Notes in Mathematics, 55) . Springer, Berlin–New York, 1975, Zweite Auflage.CrossRefGoogle Scholar
Guillarmou, C.. Lens rigidity for manifolds with hyperbolic trapped set. J. Amer. Math. Soc. (2014), to appear, arXiv:1412.1760.Google Scholar
Hofer, H.. A geometric description of the neighbourhood of a critical point given by the mountain-pass theorem. J. Lond. Math. Soc. (2) 31(3) (1985), 566–570.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54) . Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Michel, R.. Sur la rigidité imposée par la longueur des géodésiques. Invent. Math. 65(1) (1981/82), 71–83.CrossRefGoogle Scholar
Milnor, J.. Morse theory. Based on Lecture Notes by M. Spivak and R. Wells (Annals of Mathematics Studies, 51) . Princeton University Press, Princeton, NJ, 1963.Google Scholar
Mukhometov, R. G.. On a problem of reconstructing Riemannian metrics. Sibirsk. Mat. Zh. 22(3) (1981), 119–135, 237.Google Scholar
Otal, J.-P.. Le spectre marqué des longueurs des surfaces à courbure négative. Ann. of Math. (2) 131(1) (1990), 151–162.CrossRefGoogle Scholar
Otal, J.-P.. Sur les longueurs des géodésiques d’une métrique à courbure négative dans le disque. Comment. Math. Helv. 65(2) (1990), 334–347.CrossRefGoogle Scholar
Paternain, G. P.. Geodesic Flows (Progress in Mathematics, 180) . Birkhäuser Boston, Boston, MA, 1999.CrossRefGoogle Scholar
Pestov, L. and Uhlmann, G.. Two dimensional compact simple Riemannian manifolds are boundary distance rigid. Ann. of Math. (2) 161(2) (2005), 1093–1110.CrossRefGoogle Scholar