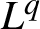Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T01:24:50.617Z Has data issue: false hasContentIssue false
  • English
  • Français

$L^{q}$-spectra of measures on planar non-conformal attractors

Part of: Basic linear algebra Classical measure theory Smooth dynamical systems: general theory

Published online by Cambridge University Press:  26 October 2020

KENNETH J. FALCONER ,
JONATHAN M. FRASER  and
LAWRENCE D. LEE
KENNETH J. FALCONER
Affiliation:
School of Mathematics & Statistics, University of St Andrews, St Andrews, KY16 9SS, UK (e-mail: [email protected], [email protected])
JONATHAN M. FRASER
Affiliation:
School of Mathematics & Statistics, University of St Andrews, St Andrews, KY16 9SS, UK (e-mail: [email protected], [email protected])
LAWRENCE D. LEE*
Affiliation:
School of Mathematics & Statistics, University of St Andrews, St Andrews, KY16 9SS, UK (e-mail: [email protected], [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the 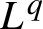$L^{q}$ -spectrum of measures in the plane generated by certain nonlinear maps. In particular, we consider attractors of iterated function systems consisting of maps whose components are 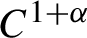$C^{1+\alpha }$ and for which the Jacobian is a lower triangular matrix at every point subject to a natural domination condition on the entries. We calculate the 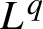$L^{q}$ -spectrum of Bernoulli measures supported on such sets by using an appropriately defined analogue of the singular value function and an appropriate pressure function.

Keywords

Lq-spectrumgeneralized q-dimensionsnon-conformal attractormodified singular value functionself-affine measure

MSC classification

Primary: 28A80: Fractals 37C45: Dimension theory of dynamical systems
Secondary: 15A18: Eigenvalues, singular values, and eigenvectors
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 11 , November 2021 , pp. 3288 - 3306
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bárány, B.. Subadditive pressure for IFS with triangular maps. Bull. Pol. Acad. Sci. Math. 57 (2009), 263–278.10.4064/ba57-3-8CrossRefGoogle Scholar
Barral, J. and Feng, D.-J.. Multifractal formalism for almost all self-affine measures. Comm. Math. Phys. 318 (2013), 473–504.10.1007/s00220-013-1676-3CrossRefGoogle Scholar
Cao, Y., Pesin, Y. and Zhao, Y.. Dimension estimates for non-conformal repellers and continuity of sub-additive topological pressure. Geom. Funct. Anal. 29 (2019), 1325–1368.10.1007/s00039-019-00510-7CrossRefGoogle Scholar
Falconer, K. J.. Bounded distortion and dimension for non-conformal repellers. Math. Proc. Cambridge Philos. Soc. 115 (1994), 315–334.10.1017/S030500410007211XCrossRefGoogle Scholar
Falconer, K. J.. Techniques in Fractal Geometry. Wiley, Chichester, 1997.Google Scholar
Falconer, K. J.. Generalised dimensions of measures on self-affine sets. Nonlinearity 12 (1999), 877–891.10.1088/0951-7715/12/4/308CrossRefGoogle Scholar
Falconer, K. J.. Generalised dimensions of measures on almost self-affine sets. Nonlinearity 23 (2010), 1047–1069.10.1088/0951-7715/23/5/002CrossRefGoogle Scholar
Falconer, K. J.. Fractal Geometry: Mathematical Foundations and Applications, 3rd edn. Wiley, Hoboken, NJ, 2014.Google Scholar
Falconer, K. J. and Miao, J.. Dimensions of self-affine fractals and multifractals generated by upper-triangular matrices. Fractals 15 (2007), 289–299.10.1142/S0218348X07003587CrossRefGoogle Scholar
Feng, D.-J. and Simon, K.. Dimension estimates for ${C}^1$ iterated function systems and repellers. Part I. Preprint, 2020, arXiv:2007.15320.10.1017/etds.2021.92CrossRefGoogle Scholar
Feng, D.-J. and Wang, Y.. A class of self-affine sets and self-affine measures. J. Fourier Anal. Appl. 11 (2005), 107–124.10.1007/s00041-004-4031-4CrossRefGoogle Scholar
Fraser, J. M.. On the ${L}^q$ -spectrum of planar self-affine measures. Trans. Amer. Math. Soc. 368 (2016), 5579–5620.10.1090/tran/6523CrossRefGoogle Scholar
Hu, H.. Dimensions of invariant sets of expanding maps. Comm. Math. Phys. 176 (1996), 307–320.10.1007/BF02099551CrossRefGoogle Scholar
Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.10.1512/iumj.1981.30.30055CrossRefGoogle Scholar
Kolossváry, I. and Simon, K.. Triangular Gatzouras-Lalley-type planar carpets with overlaps. Nonlinearity 32 (2019), 3294–3341.10.1088/1361-6544/ab1757CrossRefGoogle Scholar
Manning, A. and Simon, K.. Subadditive pressure for triangular maps. Nonlinearity 20 (2007), 133–149.10.1088/0951-7715/20/1/009CrossRefGoogle Scholar
Ngai, S.-M.. A dimension result arising from the ${L}^q$ -spectrum of a measure. Proc. Amer. Math. Soc. 125 (1997), 2943–2951.10.1090/S0002-9939-97-03974-9CrossRefGoogle Scholar
Olsen, L.. A multifractal formalism. Adv. Math. 116 (1995), 82–196.10.1006/aima.1995.1066CrossRefGoogle Scholar
Peres, Y. and Solomyak, B.. Existence of ${L}^q$ -dimensions and entropy dimension for self-conformal measures. Indiana Univ. Math. J. 49 (2000), 1603–1621.10.1512/iumj.2000.49.1851CrossRefGoogle Scholar