Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T19:15:03.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower bound in the Roth theorem for amenable groups

Published online by Cambridge University Press:  03 July 2014

QING CHU  and
PAVEL ZORIN-KRANICH Open the ORCID record for PAVEL ZORIN-KRANICH [Opens in a new window]
QING CHU
Affiliation:
Department of Mathematics, The Ohio State University, 100 Math Tower, 231 West 18th Avenue, Columbus, OH 43210-1174, USA email [email protected]
PAVEL ZORIN-KRANICH
Affiliation:
Institute of Mathematics, Hebrew University, Givat Ram, Jerusalem, 91904, Israel email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 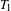$T_{1}$ and 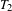$T_{2}$ be two commuting probability measure-preserving actions of a countable amenable group such that the group spanned by these actions acts ergodically. We show that 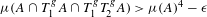${\it\mu}(A\cap T_{1}^{g}A\cap T_{1}^{g}T_{2}^{g}A)>{\it\mu}(A)^{4}-{\it\epsilon}$ on a syndetic set for any measurable set $A$ and any 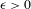${\it\epsilon}>0$. The proof uses the concept of a sated system, introduced by Austin.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 6 , September 2015 , pp. 1746 - 1766
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajtai, M. and Szemerédi, E.. Sets of lattice points that form no squares. Stud. Sci. Math. Hungar. 9(1974) (1975), 9–11.Google Scholar
Auslander, J.. Minimal Flows and their Extensions (North-Holland Mathematics Studies, 153). North-Holland Publishing Co., Amsterdam, 1988. Notas de Matemática [Mathematical Notes], 122.Google Scholar
Austin, T.. Non-conventional ergodic averages for several commuting actions of an amenable group. Preprint, September 2013.Google Scholar
Austin, T.. On the norm convergence of non-conventional ergodic averages. Ergod. Th. & Dynam. Sys. 30(2) (2010), 321–338.CrossRefGoogle Scholar
Austin, T. D.. Multiple recurrence and the structure of probability-preserving systems. PhD Thesis, University of California, Los Angeles, 2010.Google Scholar
Bergelson, V.. Ergodic theory and Diophantine problems. Topics in Symbolic Dynamics and Applications (Temuco, 1997) (London Mathematical Society Lecture Note Series, 279). Cambridge University Press, Cambridge, 2000, pp. 167–205.Google Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303, With an appendix by Imre Ruzsa.CrossRefGoogle Scholar
Bergelson, V., McCutcheon, R. and Zhang, Q.. A Roth theorem for amenable groups. Amer. J. Math. 119(6) (1997), 1173–1211.CrossRefGoogle Scholar
Chu, Q.. Multiple recurrence for two commuting transformations. Ergod. Th. & Dynam. Sys. 31(3) (2011), 771–792.CrossRefGoogle Scholar
Dye, H. A.. On the ergodic mixing theorem. Trans. Amer. Math. Soc. 118 (1965), 123–130.CrossRefGoogle Scholar
Folland, G. B.. A Course in Abstract Harmonic Analysis (Studies in Advanced Mathematics). CRC Press, Boca Raton, FL, 1995.Google Scholar
Frantzikinakis, N.. Multiple ergodic averages for three polynomials and applications. Trans. Amer. Math. Soc. 360(10) (2008), 5435–5475.CrossRefGoogle Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures). Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.CrossRefGoogle Scholar
Griesmer, J. T.. Multiparameter ergodic averages for two commuting actions of an amenable group. Preprint, 2008.Google Scholar
Hewitt, E. and Ross, K. A.. Structure of topological groups, integration theory, group representations. Abstract Harmonic Analysis, Vol. I (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 115), 2nd edn. Springer, Berlin, 1979.CrossRefGoogle Scholar
Host, B.. Ergodic seminorms for commuting transformations and applications. Studia Math. 195(1) (2009), 31–49.CrossRefGoogle Scholar
Paterson, A. L. T.. Amenability (Mathematical Surveys and Monographs, 29). American Mathematical Society, Providence, RI, 1988.CrossRefGoogle Scholar
Pedersen, G. K.. C ∗ -Algebras and their Automorphism Groups (London Mathematical Society Monographs, 14). Academic Press Inc. [Harcourt Brace Jovanovich Publishers], London, 1979.Google Scholar
Robertson, D.. Characteristic factors for commuting actions of amenable groups. J. Anal. Math. (2014), to appear.Google Scholar
Roth, K. F.. On certain sets of integers. J. Lond. Math. Soc. 28 (1953), 104–109.CrossRefGoogle Scholar
Tao, T.. A correspondence principle between (hyper)graph theory and probability theory, and the (hyper)graph removal lemma. J. Anal. Math. 103 (2007), 1–45.CrossRefGoogle Scholar
Zorin-Kranich, P.. Norm convergence of multiple ergodic averages on amenable groups. J. Anal. Math. (2014), to appear.Google Scholar