Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T03:18:36.287Z Has data issue: false hasContentIssue false
  • English
  • Français

A lower bound for topological entropy of generic non-Anosov symplectic diffeomorphisms

Published online by Cambridge University Press:  03 April 2013

THIAGO CATALAN  and
ALI TAHZIBI
THIAGO CATALAN
Affiliation:
Faculdade de Matemática, Universidade Federal de Uberlândia, Uberlândia-MG, Brazil email [email protected]
ALI TAHZIBI
Affiliation:
Instituto de Ciências, Matemática e Computação, Universidade de São Paulo, São Carlos-SP, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that a 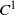${C}^{1} $ generic symplectic diffeomorphism is either Anosov or its topological entropy is bounded from below by the supremum over the smallest positive Lyapunov exponent of its periodic points. We also prove that 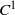${C}^{1} $ generic symplectic diffeomorphisms outside the Anosov ones do not admit symbolic extension and, finally, we give examples of volume preserving surface diffeomorphisms which are not points of upper semicontinuity of the entropy function in the 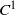${C}^{1} $ topology.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 5 , October 2014 , pp. 1503 - 1524
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F., Bonatti, C. and Crovisier, S.. Nonunifom hyperbolicity for ${C}^{1} $-generic diffeomorphisms. Israel J. Math. 183 (2011), 1–60.Google Scholar
Arbieto, A. and Catalan, T.. Hyperbolicity in the volume preserving scenario. Ergod. Th. & Dynam. Sys., available on CJO2012 doi:10.1017/etds.2012.111.CrossRefGoogle Scholar
Arbieto, A. and Matheus, C.. A pasting lemma and some applications for conservative systems. Ergod. Th. & Dynam. Sys. 27 (2007), 1399–1417.Google Scholar
Arnaud, M.-C.. Le ‘closing lemma’ en topologie ${C}^{1} $. Mém. Soc. Math. France (N.S.) 74 (1998), vi+120pp.Google Scholar
Avila, A.. On the regularization of conservative maps. Acta Math. 205 (1) (2012), 5–18.Google Scholar
Bowen, R.. Topological Entropy and Axiom A (Proceedings Symposium Pure Mathematics, 14). American Mathematical Society, Providence, RI, 1970, pp. 23–41.Google Scholar
Boyle, M., Fiebig, D. and Fiebig, U.. Residual entropy, conditional entropy, and subshift covers. Forum Math. 14 (2002), 713–757.Google Scholar
Burguet, D.. ${C}^{2} $ surface diffeomorphisms have symbolic extensions. Invent. Math. 186 (2011), 191–236.Google Scholar
Burguet, D. and Fisher, T.. Symbolic extensions for partially hyperbolic dynamical systems with 2-dimensional center bundle. Discrete Contin. Dyn. Syst. 33 (6) (2013), 2253–2270.Google Scholar
Buzzi, J.. Intrinsic ergodicity for smooth interval maps. Israel J. Math. 100 (1997), 125–161.CrossRefGoogle Scholar
Diaz, L. and Fisher, T.. Symbolic extensions for partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 29 (4) (2011), 1419–1441.Google Scholar
Diaz, L., Fisher, T., Pacífico, M. and Vieitez, J.. Entropy-expansiveness for partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 32 (2012), 4195–4207.Google Scholar
Kaloshin, V.. An extension of the Artin–Mazur theorem. Ann. of Math. (2) 150 (2) (1999), 729–741.CrossRefGoogle Scholar
Katok, A.. Lyapunov exponents, entropy and periodic points for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.Google Scholar
Liang, C., Liu, G. and Sun, W.. Equivalent conditions of dominated splittings for volume-preserving diffeomorphism. Acta Math. Sinica 23 (2007), 1563–1576.Google Scholar
Gonchenko, S. V., Turaev, D. V. and Shilnikov, L. P.. Homoclinic tangencies of arbitrarily high orders in conservative and dissipative two-dimensional maps. Nonlinearity 20 (2) (2007), 241–275.Google Scholar
Gonchenko, S. V., Turaev, D. V. and Shilnikov, L. P.. On dynamical properties of diffeomorphisms with homoclinic tangencies. Contemp. Math. Appl. 7 (2003), 92–118.Google Scholar
Misiurewicz, M.. On non-continuity of topological entropy. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astron. Phys. 19 (1971), 319–320.Google Scholar
Downarowicz, T. and Newhouse, S. E.. Symbolic extension and smooth dynamical systems. Invent. Math. 160 (2005), 453–499.Google Scholar
Newhouse, S. E.. Topological entropy and Hausdorff dimension for area preserving diffeomorphisms of surfaces. Astérisque 51 (1978), 323–334.Google Scholar
Newhouse, S. E.. Quasi-elliptic periodic points in conservative dynamical systems. Amer. J. Math. 99 (5) (1975), 1061–1087.Google Scholar
Palis, J. and Takens, F.. Hyperbolicity and Sensitive-chaotic Dynamics at Homoclinic Bifurcations (Cambridge Studies in Advanced Mathematics, 35). Cambridge University Press, Cambridge, 1993.Google Scholar
Rees, M.. A minimal positive entropy homeomorphism of the 2-torus. J. Lond. Math. Soc. (2) 23 (3) (1981), 537–550.Google Scholar
Xia, Z.. Homoclinic points in symplectic and volume-preserving diffeomorphisms. Commun. Math. Phys. 177 (1996), 435–449.Google Scholar
Young, L. S.. Entropy of continuous flows on compact 2-manifolds. Topology 16 (4) (1977), 469–471.Google Scholar
Zehnder, E.. Note on smoothing symplectic and volume-preserving diffeomorphisms. Geometry and Topology (Proc. III Latin Amer. School of Math., Inst. Mat. Pura Aplicada CNPq, Rio de Janeiro, 1976) (Lecture Notes in Mathematics, 597). Springer, Berlin, 1977, pp. 828–854.Google Scholar