Article contents
Lower and upper bounds for the Lyapunov exponents of twisting dynamics: a relationship between the exponents and the angle of Oseledets’ splitting
Published online by Cambridge University Press: 17 April 2012
Abstract
We consider locally minimizing measures for conservative twist maps of the 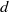 $d$-dimensional annulus and for Tonelli Hamiltonian flows defined on a cotangent bundle
$d$-dimensional annulus and for Tonelli Hamiltonian flows defined on a cotangent bundle 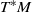 $T^*M$. For weakly hyperbolic measures of such type (i.e. measures with no zero Lyapunov exponents), we prove that the mean distance/angle between the stable and unstable Oseledets bundles gives an upper bound on the sum of the positive Lyapunov exponents and a lower bound on the smallest positive Lyapunov exponent. We also prove some more precise results.
$T^*M$. For weakly hyperbolic measures of such type (i.e. measures with no zero Lyapunov exponents), we prove that the mean distance/angle between the stable and unstable Oseledets bundles gives an upper bound on the sum of the positive Lyapunov exponents and a lower bound on the smallest positive Lyapunov exponent. We also prove some more precise results.
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 4
- Cited by


