Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T15:38:12.474Z Has data issue: false hasContentIssue false
  • English
  • Français

The local rotation set is an interval

Published online by Cambridge University Press:  04 May 2017

JONATHAN CONEJEROS
JONATHAN CONEJEROS*
Affiliation:
Institut de Mathématiques de Jussieu – Paris Rive Gauche, UPMC, 4 place Jussieu, Case 247, 75252 Paris Cedex 5, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 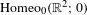$\text{Homeo}_{0}(\mathbb{R}^{2};0)$ be the set of all homeomorphisms of the plane that are isotopic to the identity and which fix zero. Recently, in Le Roux [L’ensemble de rotation autour d’un point fixe. Astérisque (350) (2013), 1–109], Le Roux gave the definition of the local rotation set of an isotopy$I$ in 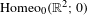$\text{Homeo}_{0}(\mathbb{R}^{2};0)$ from the identity to a homeomorphism 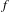$f$ and he asked if this set is always an interval. In this article, we give a positive answer to this question and to the analogous question in the case of the open annulus.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 7 , October 2018 , pp. 2571 - 2617
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Dávalos, P.. On torus homeomorphisms whose rotation set is an interval. Math. Z. 275(3–4) (2013), 1005–1045.Google Scholar
de Melo, W. and Palis, J. Jr.. Geometric Theory of Dynamical Systems: An Introduction. Springer, New York, 1982.Google Scholar
Franks, J. and Misiurewicz, M.. Rotation sets of toral flows. Proc. Amer. Math. Soc. 109(1) (1990), 243–249.Google Scholar
Franks, J.. Generalizations of the Poincaré–Birkhoff theorem. Ann. of Math. (2) 128(1) (1988), 139–151.Google Scholar
Franks, J.. Area preserving homeomorphisms of open surfaces of genus zero. New York J. Math. 2 (1996), 1–19.Google Scholar
Gambaudo, J.-M. and Pécou, É.. A topological invariant for volume preserving diffeomorphisms. Ergod. Th. & Dynam. Sys. 15(3) (1995), 535–541.Google Scholar
Haefliger, A.. Variétés feuilletées. Ann. Sc. Norm. Super. Pisa (3) 16(4) (1962), 367–397.Google Scholar
Hamströn, M.-E.. Homotopy in homeomorphism spaces, TOP and PL. Bull. Amer. Math. Soc. (N.S.) 80 (1974), 207–230.Google Scholar
Le Calvez, P.. Propriétés dynamiques des difféomorphismes de l’anneau et du tore. Astérisque (204) (1991), 1–131.Google Scholar
Le Calvez, P.. Rotation numbers in the infinite annulus. Proc. Amer. Math. Soc. 129(11) (2001), 3221–3230.Google Scholar
Le Calvez, P.. Dynamique des homéomorphismes du plan au voisinage d’un point fixe. Ann. Sc. Éc. Norm. Supér. (4) 36(1) (2003), 139–171.Google Scholar
Le Calvez, P.. Une version feuilletée équivariante du théorème de translation de Brouwer. Publ. Math. Inst. Hautes Études Sci. (102) (2005), 1–98.Google Scholar
Le Calvez, P.. Pourquoi les points périodiques des homéomorphismes du plan tournent-ils autour de certains points fixes? Ann. Sc. Éc. Norm. Supér. (4) 41(1) (2008), 141–176.Google Scholar
Le Roux, F.. Migration des points errants d’un homéomorphisme de surface. C. R. Math. Acad. Sci. Paris, Sér. I 330(3) (2000), 225–230.Google Scholar
Le Roux, F.. Homéomorphismes de surfaces: théorèmes de la fleur de Leau-Fatou et de la variété stable. Astérisque (292) (2004), 1–120.Google Scholar
Le Roux, F.. L’ensemble de rotation autour d’un point fixe. Astérisque (350) (2013), 1–109.Google Scholar
Llibre, J. and MacKay, R. S.. Rotation vectors and entropy for homeomorphisms of the torus isotopic to the identity. Ergod. Th. & Dynam. Sys. 11(1) (1991), 115–128.Google Scholar
Le Calvez, P. and Tal, F. A.. Forcing theory for transverse trajectories of surface homeomorphisms. Preprint, 2015, arXiv:1503.09127 (e-print).Google Scholar
Le Calvez, P. and Yoccoz, J.-C.. Un théorème d’indice pour les homéomorphismes du plan au voisinage d’un point fixe. Ann. of Math. (2) 146(2) (1997), 241–293.Google Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. 40(2) (1989), 490–506.Google Scholar
Naĭshul’, V. A.. Topological invariants of analytic and area-preserving mappings and their application to analytic differential equations in C 2 and C P 2 . Tr. Mosk. Mat. Obs. 44 (1982), 235–245.Google Scholar
Poincaré, H.. Mémoire sur les courbes définies par une équation différentielle, chapitre XV. J. Math. Pures Appl. Série IV (1) (1885), 167–244.Google Scholar
Wang, J.. A generalization of the line translation theorem. Trans. Amer. Math. Soc. 366(11) (2014), 5903–5923.Google Scholar
Whitney, H.. Regular families of curves. Ann. of Math. (2) 34(2) (1933), 244–270.Google Scholar
Whitney, H.. On regular families of curves. Bull. Amer. Math. Soc. 47 (1941), 145–147.Google Scholar