Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T16:24:22.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear equations over multiplicative groups, recurrences, and mixing III

Published online by Cambridge University Press:  02 May 2017

H. DERKSEN  and
D. MASSER
H. DERKSEN
Affiliation:
Department of Mathematics, University of Michigan, East Hall, 530 Church Street, Ann Arbor, Michigan 48104, USA email [email protected]
D. MASSER
Affiliation:
Departement Mathematik und Informatik, Universität Basel, Spiegelgasse 1, 4051 Basel, Switzerland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given an algebraic 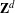$\mathbf{Z}^{d}$-action corresponding to a prime ideal of a Laurent ring of polynomials in several variables, we show how to find the smallest order 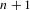$n+1$ of non-mixing. It is known that this is determined by the non-mixing sets of size 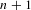$n+1$, and we show how to find these in an effective way. When the underlying characteristic is positive and 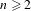$n\geq 2$, we prove that there are at most finitely many classes under a natural equivalence relation. We work out two examples, the first with five classes and the second with 134 classes.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 7 , October 2018 , pp. 2625 - 2643
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arenas-Carmona, L., Berend, D. and Bergelson, V.. Ledrappier’s system is almost mixing of all orders. Ergod. Th. & Dynam. Sys. 28 (2008), 339–365.Google Scholar
Brownawell, W. D. and Masser, D.. Vanishing sums in function fields. Math. Proc. Cambridge Philos. Soc. 100 (1986), 427–434.Google Scholar
Bombieri, E., Masser, D. and Zannier, U.. Anomalous subvarieties—structure theorems and applications. Int. Math. Res. Not. IMRN (2007), Article ID rnm057 (33 pages), doi:10.1093/imrn/rnm057.Google Scholar
Derksen, H.. A Skolem–Mahler–Lech theorem in positive characteristic and finite automata. Invent. Math. 168 (2007), 175–224.Google Scholar
Derksen, H. and Masser, D.. Linear equations over multiplicative groups, recurrences, and mixing I. Proc. Lond. Math. Soc. 104 (2012), 1045–1083.Google Scholar
Derksen, H. and Masser, D.. Linear equations over multiplicative groups, recurrences, and mixing II. Indag. Math. 26 (2015), 113–136.Google Scholar
Ledrappier, F.. Un champ markovien peut être d’entropie nulle et mélangeant. C. R. Math. Acad. Sci. Paris 287 (1978), 561–563.Google Scholar
Leitner, D.. Linear equations over multiplicative groups in positive characteristic. Acta Arith. 153 (2012), 325–347.Google Scholar
Loher, T. and Masser, D.. Uniformly counting points of bounded height. Acta Arith. 111 (2004), 277–297.Google Scholar
Masser, D.. Mixing and linear equations over groups in positive characteristic. Israel J. Math. 142 (2004), 189–204.Google Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin. Birkhäuser, Basel, 1995.Google Scholar
Schlickewei, H. P. and Viola, C.. Polynomials that divide many k-nomials. Number Theory in Progress. Eds. Györy, K., Iwaniec, H. and Urbanowicz, J.. Walter de Gruyter, Berlin, 1999, pp. 445–450.Google Scholar
Schmidt, K. and Ward, T.. Mixing automorphisms of compact groups and a theorem of Schlickewei. Invent. Math. 111 (1993), 69–76.Google Scholar
Ward, T.. Three results on mixing shapes. New York J. Math. 3A (1997), 1–10.Google Scholar