Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T03:10:15.695Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit drift

Published online by Cambridge University Press:  04 July 2016

GENADI LEVIN  and
GRZEGORZ ŚWIA̧TEK
GENADI LEVIN
Affiliation:
Einstein Institute of Mathematics, Hebrew University, Givat Ram 91904, Jerusalem, Israel email [email protected]
GRZEGORZ ŚWIA̧TEK
Affiliation:
Department of Mathematics and Information Science, Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, Poland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the problem of the existence of wild attractors for critical circle coverings with Fibonacci dynamics. This is known to be related to the drift for the corresponding fixed points of renormalization. The fixed point depends only on the order of the critical point 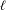$\ell$ and its drift is a number 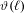$\unicode[STIX]{x1D717}(\ell )$ which is finite for each finite 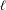$\ell$. We show that the limit 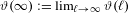$\unicode[STIX]{x1D717}(\infty ):=\lim _{\ell \rightarrow \infty }\unicode[STIX]{x1D717}(\ell )$ exists and is finite. The finiteness of the limit is in a sharp contrast with the case of Fibonacci unimodal maps. Furthermore, 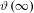$\unicode[STIX]{x1D717}(\infty )$ is expressed as a contour integral in terms of the limit of the fixed points of renormalization when 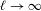$\ell \rightarrow \infty$. There is a certain paradox here, since this dynamical limit is a circle homeomorphism with the golden mean rotation number whose own drift is 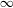$\infty$ for topological reasons.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 8 , December 2017 , pp. 2643 - 2670
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bruin, H.. Topological conditions for the existence of absorbing Cantor sets. Trans. Amer. Math. Soc. 350 (1998), 2229–2263.Google Scholar
Bruin, H., Keller, G., Nowicki, T. and Van Strien, S.. Wild Cantor attractors exist. Ann. of Math. (2) 143 (1996), 97–130.CrossRefGoogle Scholar
Buff, X.. Fibonacci fixed points of renormalization. Ergod. Th. & Dynam. Sys. 20 (2000), 1287–1317.Google Scholar
Buff, X. and Cheritat, A.. Quadratic Julia sets with positive area. Ann. of Math. (2) 176(2) (2012), 673–746.Google Scholar
Epstein, H.. Fixed Points of the Period-doubling Operator (Lecture Notes). Lausanne, 1992.Google Scholar
Levin, G. and Świa̧tek, G.. Universality of critical circle covers. Comm. Math. Phys. 228 (2002), 371–399.Google Scholar
Levin, G. and Świa̧tek, G.. Dynamics and universality of unimodal mappings with infinite criticality. Comm. Math. Phys. 258 (2005), 103–133.Google Scholar
Levin, G. and Świa̧tek, G.. Common limits of Fibonacci circle maps. Comm. Math. Phys. 312 (2012), 695–734.Google Scholar
McMullen, C.. Renormalization and 3-manifolds Which Fiber Over the Circle (Annals of Mathematics Studies, 142) . Princeton University Press, Princeton, NJ, 1998.Google Scholar
Moreira, C. G. and Smania, D.. Metric stability for random walks (with applications in renormalization theory). Frontiers in Complex Dynamics (Princeton Mathematical Series, 51) . Princeton University Press, Princeton, NJ, 2014, pp. 261–322.Google Scholar
Van Strien, S. and Nowicki, T.. Polynomial maps with a Julia set of positive Lebesgue measure: Fibonacci maps. Preprint, arXiv:math/9402215.Google Scholar