Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:01:04.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Leaf conjugacies on the torus

Published online by Cambridge University Press:  29 January 2013

ANDY HAMMERLINDL
ANDY HAMMERLINDL*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, Canada M5S 2E4 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

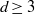If a partially hyperbolic diffeomorphism on a torus of dimension $d\geq 3$ has stable and unstable foliations which are quasi-isometric on the universal cover, and its centre direction is one-dimensional, then the diffeomorphism is leaf conjugate to a linear toral automorphism. In other words, the hyperbolic structure of the diffeomorphism is exactly that of a linear, and thus simple to understand, example. In particular, every partially hyperbolic diffeomorphism on the 3-torus is leaf conjugate to a linear toral automorphism.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 3 , June 2013 , pp. 896 - 933
Copyright
Copyright ©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E.. The General Topology of Dynamical Systems. American Mathematical Society, Providence, RI, 1993.Google Scholar
Anosov, D. V.. Geodesic flows on closed Riemann manifolds with negative curvature. Proc. Steklov Inst. Math. 90 (1967), 1–235.Google Scholar
Bonatti, C. and Wilkinson, A.. Transitive partially hyperbolic diffeomorphisms on 3-manifolds. Topology 44 (3) (2005), 475–508.CrossRefGoogle Scholar
Brin, M.. On dynamical coherence. Ergod. Th. & Dynam. Sys. 23 (2003), 395–401.Google Scholar
Brin, M., Burago, D. and Ivanov, S.. On partially hyperbolic diffeomorphisms of 3-manifolds with commutative fundamental group. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 307–312.Google Scholar
Brin, M., Burago, D. and Ivanov, S.. Dynamical coherence of partially hyperbolic diffeomorphisms of the 3-torus. J. Mod. Dyn. 3 (1) (2009), 1–11.Google Scholar
Brin, M. and Pesin, Ja.. Partially hyperbolic dynamical systems. Math. USSR Izv. 8 (1974), 177–218.Google Scholar
Burago, D. and Ivanov, S.. Partially hyperbolic diffeomorphisms of 3-manifolds with abelian fundamental groups. J. Mod. Dyn. 2 (4) (2008), 541–580.Google Scholar
Burns, K. and Wilkinson, A.. Dynamical coherence and center bunching. Discrete Contin. Dyn. Syst. 22 (1&2) (2008), 89–100.Google Scholar
Fenley, S. R.. Quasi-isometric foliations. Topology 31 (3) (1992), 667–676.Google Scholar
Franks, J.. Anosov diffeomorphisms on tori. Trans. Amer. Math. Soc. 145 (1969), 117–124.CrossRefGoogle Scholar
Franks, J.. Anosov diffeomorphisms. Global Analysis (Proc. Sympos. Pure Math., 14). American Mathematical Society, Providence, RI, 1970, pp. 61–93.Google Scholar
Hammerlindl, A.. Quasi-isometry and plaque expansiveness. Canad. Math. Bull. 54 (2011), 676–679.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A. and Ures, R.. Accessibility and stable ergodicity for partially hyperbolic diffeomorphisms with 1d-center bundle. Invent. Math. 172 (2) (2008), 353–381.Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer, Berlin, 1977.CrossRefGoogle Scholar
Manning, A.. There are no new Anosov diffeomorphisms on tori. Amer. J. Math. 96 (3) (1974), 422–42.Google Scholar
Pugh, C., Shub, M. and Wilkinson, A.. Hölder foliations. Duke Math. J. 86 (3) (1997), 517–546.Google Scholar