Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T16:49:42.676Z Has data issue: false hasContentIssue false
  • English
  • Français

${\it\alpha}$-Hölder linearization of hyperbolic diffeomorphisms with resonance

Published online by Cambridge University Press:  11 August 2014

WENMENG ZHANG  and
WEINIAN ZHANG
WENMENG ZHANG
Affiliation:
College of Mathematics Science, Chongqing Normal University, Chongqing 400047, PR China email [email protected], [email protected]
WEINIAN ZHANG
Affiliation:
Yangtze Center of Mathematics and Department of Mathematics, Sichuan University, Chengdu, Sichuan 610064, PR China
Get access Rights & Permissions [Opens in a new window]

Abstract

Concerning hyperbolic diffeomorphisms, one expects a better smoothness of linearization, but it may be confined by resonance among eigenvalues. Hartman gave a three-dimensional analytic mapping with resonance which cannot be linearized by a Lipschitz conjugacy. Since then, efforts have been made to give the ${\it\alpha}$-Hölder continuity of the conjugacy and hope the exponent ${\it\alpha}<1$ can be as large as possible. Recently, it was proved for some weakly resonant hyperbolic diffeomorphisms that ${\it\alpha}$ can be as large as we expect. In this paper we prove that this result holds for all 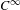$C^{\infty }$ weakly resonant hyperbolic diffeomorphisms.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 1 , February 2016 , pp. 310 - 334
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barreira, L. and Valls, C.. Hölder Grobman-Hartman linearization. Discrete Contin. Dyn. Syst. 18 (2007), 187–197.CrossRefGoogle Scholar
Bates, P. W., Lu, K. and Zeng, C.. Invariant foliations near normally hyperbolic invariant manifolds for semiflows. Trans. Amer. Math. Soc. 352 (2000), 4641–4676.CrossRefGoogle Scholar
Belitskii, G. R.. Equivalence and normal forms of germs of smooth mappings. Russian Math. Surveys 33 (1978), 107–177.CrossRefGoogle Scholar
Bronstein, I. U. and Kopanski, A. Ya.. Smooth Invariant Manifolds and Normal Forms. World Scientific, River Edge, NJ, 1994.CrossRefGoogle Scholar
Chen, X.-Y., Hale, J. K. and Tan, B.. Invariant foliations for C 1 semigroups in Banach spaces. J. Differential Equations 139 (1997), 283–318.CrossRefGoogle Scholar
Chow, S. N., Li, C. and Wang, D.. Normal Forms and Bifurcation of Planar Vector Fields. Cambridge University Press, Cambridge, 1994.CrossRefGoogle Scholar
Guysinsky, M., Hasselblatt, B. and Rayskin, V.. Differentiability of the Hartman–Grobman linearization. Discrete Contin. Dyn. Syst. 9 (2003), 979–984.CrossRefGoogle Scholar
Hartman, P.. On local homeomorphisms of Euclidean spaces. Bol. Soc. Mat. Mexicana 5 (1960), 220–241.Google Scholar
Hartman, P.. A lemma in the theory of structural stability of differential equations. Proc. Amer. Math. Soc. 11 (1960), 610–620.CrossRefGoogle Scholar
Hirsch, M., Shub, M. and Pugh, C.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer, New York, 1977.CrossRefGoogle Scholar
Lawson, H. B.. Foliations. Bull. Amer. Math. Soc. 80 (1974), 369–418.CrossRefGoogle Scholar
Rayskin, V.. 𝛼-Hölder linearization. J. Differential Equations 147 (1998), 271–284.CrossRefGoogle Scholar
Rudin, W.. Principles of Mathematical Analysis, 3rd edn. McGraw-Hill, New York, 1976.Google Scholar
Rudin, W.. Functional Analysis, 2nd edn. McGraw-Hill, New York, 1991.Google Scholar
Sell, G. R.. Smooth linearization near a fixed point. Amer. J. Math. 107 (1985), 1035–1091.CrossRefGoogle Scholar
Sternberg, S.. Local contractions and a theorem of Poincaré. Amer. J. Math. 79 (1957), 809–824.CrossRefGoogle Scholar
Sternberg, S.. On the structure of local homeomorphisms of Euclidean m-space. Amer. J. Math. 80 (1958), 623–631.CrossRefGoogle Scholar
Strien, S.. Smooth linearization of hyperbolic fixed points without resonance conditions. J. Differential Equations 85 (1990), 66–90.CrossRefGoogle Scholar
Tan, B.. 𝜎-Hölder continuous linearization near hyperbolic fixed points in ℝn. J. Differential Equations 162 (2000), 251–269.CrossRefGoogle Scholar
Zhang, W. M. and Zhang, W. N.. C 1 linearization for planar contractions. J. Funct. Anal. 260 (2011), 2043–2063.CrossRefGoogle Scholar
Zhang, W. M., Zhang, W. N. and Jarczyk, W.. Sharp regularity of linearization for C 1, 1 hyperbolic diffeomorphisms. Math. Ann. 358 (2014), 69–113.CrossRefGoogle Scholar
Zhang, W. N.. Invariant foliations for parabolic equations. Sci. China Ser. A 43 (2000), 357–370.CrossRefGoogle Scholar