Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T00:41:42.391Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant coupling of determinantal measures on sofic groups

Published online by Cambridge University Press:  05 August 2014

RUSSELL LYONS  and
ANDREAS THOM
RUSSELL LYONS
Affiliation:
Department of Mathematics, 831 East 3rd Street, Indiana University, Bloomington, IN 47405-7106, USA email [email protected]
ANDREAS THOM
Affiliation:
Mathematics Institute, University of Leipzig, PF 100920, D-04009 Leipzig, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

To any positive contraction 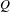$Q$ on 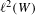$\ell ^{2}(W)$, there is associated a determinantal probability measure 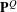$\mathbf{P}^{Q}$ on 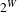$2^{W}$, where 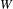$W$ is a denumerable set. Let ${\rm\Gamma}$ be a countable sofic finitely generated group and 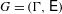$G=({\rm\Gamma},\mathsf{E})$ be a Cayley graph of ${\rm\Gamma}$. We show that if 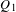$Q_{1}$ and 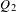$Q_{2}$ are two ${\rm\Gamma}$-equivariant positive contractions on 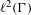$\ell ^{2}({\rm\Gamma})$ or on 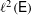$\ell ^{2}(\mathsf{E})$ with 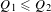$Q_{1}\leq Q_{2}$, then there exists a ${\rm\Gamma}$-invariant monotone coupling of the corresponding determinantal probability measures witnessing the stochastic domination $\mathbf{P}^{Q_{1}}\preccurlyeq \mathbf{P}^{Q_{2}}$. In particular, this applies to the wired and free uniform spanning forests, which was known before only when ${\rm\Gamma}$ is residually amenable. In the case of spanning forests, we also give a second more explicit proof, which has the advantage of showing an explicit way to create the free uniform spanning forest as a limit over a sofic approximation. Another consequence of our main result is to prove that all determinantal probability measures $\mathbf{P}^{Q}$ as above are 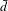$\bar{d}$-limits of finitely dependent processes. Thus, when ${\rm\Gamma}$ is amenable, 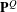$\mathbf{P}^{Q}$ is isomorphic to a Bernoulli shift, which was known before only when ${\rm\Gamma}$ is abelian. We also prove analogous results for sofic unimodular random rooted graphs.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 2 , April 2016 , pp. 574 - 607
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abért, M. and Weiss, B.. Bernoulli actions are weakly contained in any free action. Ergod. Th. & Dynam. Sys. 33(2) (2013), 323–333.CrossRefGoogle Scholar
Abért, M., Virág, B. and Thom, A.. Benjamini-Schramm convergence and pointwise convergence of the spectral measure. Preprint, 2011, http://www.math.uni-leipzig.de/MI/thom/.Google Scholar
Adams, S.. Very weak Bernoulli for amenable groups. Israel J. Math. 78(2–3) (1992), 145–176.CrossRefGoogle Scholar
Aldous, D. J. and Lyons, R.. Processes on unimodular random networks. Electron. J. Probab. 12(54) (2007), 1454–1508 (electronic).CrossRefGoogle Scholar
Bekka, M. and Valette, A.. Group cohomology, harmonic functions and the first L 2 -Betti number. Potential Anal. 6(4) (1997), 313–326.CrossRefGoogle Scholar
Benjamini, I., Lyons, R., Peres, Y. and Schramm, O.. Uniform spanning forests. Ann. Probab. 29 (2001), 1–65.CrossRefGoogle Scholar
Benjamini, I. and Schramm, O.. Recurrence of distributional limits of finite planar graphs. Electron. J. Probab. 6(23) (2001), 13 (electronic).CrossRefGoogle Scholar
Borcea, J., Brändén, P. and Liggett, T. M.. Negative dependence and the geometry of polynomials. J. Amer. Math. Soc. 22 (2009), 521–567.CrossRefGoogle Scholar
Bowen, L.. Couplings of uniform spanning forests. Proc. Amer. Math. Soc. 132(7) (2004), 2151–2158.CrossRefGoogle Scholar
Bowen, L.. Measure conjugacy invariants for actions of countable sofic groups. J. Amer. Math. Soc. 23(1) (2010), 217–245.CrossRefGoogle Scholar
Brooks, R. L., Smith, C. A. B., Stone, A. H. and Tutte, W. T.. The dissection of rectangles into squares. Duke Math. J. 7 (1940), 312–340.CrossRefGoogle Scholar
Brown, N. and Ozawa, N.. C ∗ -Algebras and Finite-Dimensional Approximations (Graduate Studies in Mathematics, 88). American Mathematical Society, Providence, RI, 2008.CrossRefGoogle Scholar
Burton, R. M. and Pemantle, R.. Local characteristics, entropy and limit theorems for spanning trees and domino tilings via transfer-impedances. Ann. Probab. 21 (1993), 1329–1371.CrossRefGoogle Scholar
Chifan, I. and Ioana, A.. Ergodic subequivalence relations induced by a Bernoulli action. Geom. Funct. Anal. 20(1) (2010), 53–67.CrossRefGoogle Scholar
Connes, A.. Classification of injective factors cases II 1 , II ∞ , III 𝜆 , 𝜆≠1. Ann. of Math. (2) 104(1) (1976), 73–115.CrossRefGoogle Scholar
Cornulier, Y.. A sofic group away from amenable groups. Math. Ann. 350(2) (2011), 269–275.CrossRefGoogle Scholar
Dixmier, J.. Von Neumann Algebras. North-Holland, Amsterdam, 1981.Google Scholar
Douglas, R. G.. On majorization, factorization, and range inclusion of operators on Hilbert space. Proc. Amer. Math. Soc. 17(2) (1966), 413–415.CrossRefGoogle Scholar
Elek, G. and Szabó, E.. Sofic groups and direct finiteness. J. Algebra 280(2) (2004), 426–434.CrossRefGoogle Scholar
Elek, G. and Szabó, E.. Hyperlinearity, essentially free actions and L 2 -invariants. The sofic property. Math. Ann. 332(2) (2005), 421–441.CrossRefGoogle Scholar
Elek, G. and Szabó, E.. On sofic groups. J. Group Theory 9(2) (2006), 161–171.CrossRefGoogle Scholar
Elek, G. and Lippner, G.. Sofic equivalence relations. J. Funct. Anal. 258(5) (2010), 1692–1708.CrossRefGoogle Scholar
Feldman, J. and Moore, C.. Ergodic equivalence relations, cohomology, and von Neumann algebras. II. Trans. Amer. Math. Soc. 234(2) (1977), 325–359.CrossRefGoogle Scholar
Fontes, L. R. G. and Mathieu, P.. On symmetric random walks with random conductances on ℤd. Probab. Theory Related Fields 134 (2006), 565–602.CrossRefGoogle Scholar
Glasner, E.. Ergodic Theory via Joinings. American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Häggström, O.. Random-cluster measures and uniform spanning trees. Stoch. Process. Appl. 59 (1995), 267–275.CrossRefGoogle Scholar
Houdayer, C.. Invariant percolation and measured theory of nonamenable groups [after Gaboriau-Lyons, Ioana, Epstein]. Astérisque 348 (2012), 339–374 . Exp. No. 1039, ix, Séminaire Bourbaki: Vol. 2010/2011. Exposés 1027–1042.Google Scholar
Kadison, R. V. and Ringrose, J. R.. Fundamentals of the Theory of Operator Algebras. Vol. I: Elementary Theory (Graduate Studies in Mathematics, 15). American Mathematical Society, Providence, RI, 1997, Reprint of the 1983 original.CrossRefGoogle Scholar
Kadison, R. V. and Ringrose, J. R.. Fundamentals of the Theory of Operator Algebras. Vol. II: Advanced Theory (Graduate Studies in Mathematics, 16). American Mathematical Society, Providence, RI, 1997, Corrected reprint of the 1986 original.CrossRefGoogle Scholar
Kulesza, A. and Taskar, B.. Determinantal point processes for machine learning. Found. Trends Mach. Learn. 5(2–3) (2012), 123–286.CrossRefGoogle Scholar
Kirchhoff, G.. Ueber die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Vertheilung galvanischer Ströme geführt wird. Ann. Phys. Chem. 72(1847) 497–508.Google Scholar
Kun, G.. Expanders have a spanning Lipschitz subgraph with large girth. Preprint, 2013, arXiv:1303.4982.Google Scholar
Lück, W.. Approximating L 2 -invariants by their finite-dimensional analogues. Geom. Funct. Anal. 4 (1994), 455–481.CrossRefGoogle Scholar
Lück, W.. L 2 -Invariants: Theory and Applications to Geometry and K-theory (Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge/A Series of Modern Surveys in Mathematics, 44). Springer, Berlin, 2002.CrossRefGoogle Scholar
Lyons, R.. A bird’s-eye view of uniform spanning trees and forests. Microsurveys in Discrete Probability (DIMACS Series in Discrete Mathematics and Theoretical Computer Science, 41). Eds. Aldous, D. and Propp, J.. American Mathematical Society, Providence, RI, 1998, pp. 135–162 Papers from the workshop held as part of the Dimacs Special Year on Discrete Probability in Princeton, NJ, June 2–6, 1997.CrossRefGoogle Scholar
Lyons, R.. Determinantal probability measures. Publ. Math. Inst. Hautes Études Sci. 98 (2003), 167–212 Errata, http://mypage.iu.edu/∼rdlyons/errata/bases.pdf.CrossRefGoogle Scholar
Lyons, R. and Steif, J.E.. Stationary determinantal processes: phase multiplicity, Bernoullicity, entropy, and domination. Duke Math. J. 120(3) (2003), 515–575.CrossRefGoogle Scholar
Lyons, R.. Fixed price of groups and percolation. Ergod. Th. & Dynam. Sys. 33(1) (2013), 183–185.CrossRefGoogle Scholar
Lyons, R.. Factors of IID on trees. Preprint, 2013, arXiv:1401.4197.Google Scholar
Macchi, O.. The coincidence approach to stochastic point processes. Adv. Appl. Probab. 7 (1975), 83–122.CrossRefGoogle Scholar
Mester, P.. Invariant monotone coupling need not exist. Ann. Probab. 41(3A) (2013), 1180–1190.CrossRefGoogle Scholar
Nielsen, O. A.. Direct Integral Theory (Lecture Notes in Pure and Applied Mathematics, 61). Marcel Dekker, New York, 1980.Google Scholar
Ornstein, D.. Factors of Bernoulli shifts are Bernoulli shifts. Adv. Math. 5 (1970), 349–364.CrossRefGoogle Scholar
Ornstein, D. S.. Ergodic Theory, Randomness, and Dynamical Systems (Lectures in Mathematics given at Yale University, Yale Mathematical Monographs, No. 5). Ed. Whittemore, J. K.. Yale University Press, New Haven, CT, 1974.Google Scholar
Ornstein, D. S. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.CrossRefGoogle Scholar
Păunescu, L.. On sofic actions and equivalence relations. J. Funct. Anal. 261(9) (2011), 2461–2485.CrossRefGoogle Scholar
Pemantle, R.. Choosing a spanning tree for the integer lattice uniformly. Ann. Probab. 19 (1991), 1559–1574.CrossRefGoogle Scholar
Peterson, J. and Thom, A.. Group cocycles and the ring of affiliated operators. Invent. Math. 185 (2011), 561–592.CrossRefGoogle Scholar
Popa, S.. Some computations of 1-cohomology groups and construction of non-orbit-equivalent actions. J. Inst. Math. Jussieu 5(2) (2006), 309–332.CrossRefGoogle Scholar
Renault, J. N.. A Groupoid Approach to C ∗ -algebras (Lecture Notes in Mathematics, 793). Springer, Berlin, 1980.CrossRefGoogle Scholar
Sauer, R.. L 2 -Betti numbers of discrete measured groupoids. Int. J. Algebra Comput. 15(5 & 6) (2005), 1169–1188.CrossRefGoogle Scholar
Skorohod, A. V.. Limit theorems for stochastic processes. Teor. Veroyatn. Primen. 1 (1956), 289–319 (in Russian). English translation in Theory Probab. Appl. 1 (1956), 261–290.Google Scholar
Soshnikov, A.. Determinantal random point fields. Uspekhi Mat. Nauk 55 (2000), 107–160.Google Scholar
Strassen, V.. The existence of probability measures with given marginals. Ann. Math. Statist. 36 (1965), 423–439.CrossRefGoogle Scholar
Takesaki, M.. Theory of Operator Algebras. III (Encyclopaedia of Mathematical Sciences, 127). Springer, Berlin, 2003.CrossRefGoogle Scholar
Thom, A.. Sofic groups and Diophantine approximation. Commun. Pure Appl. Math. 61(8) (2008), 1155–1171.CrossRefGoogle Scholar
Weiss, B.. Sofic groups and dynamical systems. Sankhyā Ser. A 62(3) (2000), 350–359.Google Scholar