Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:51:54.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant circles and depinning transition

Published online by Cambridge University Press:  22 September 2016

WEN-XIN QIN  and
YA-NAN WANG
WEN-XIN QIN
Affiliation:
Department of Mathematics, Soochow University, Suzhou215006, China email [email protected]
YA-NAN WANG
Affiliation:
School of Mathematical Sciences, Fudan University, Shanghai200433, China
Get access Rights & Permissions [Opens in a new window]

Abstract

We associate the existence or non-existence of rotational invariant circles of an area-preserving twist map on the cylinder with a physically motivated quantity, the depinning force, which is a critical value in the depinning transition. Assume that 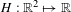$H:\mathbb{R}^{2}\mapsto \mathbb{R}$ is a 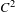$C^{2}$ generating function of an exact area-preserving twist map 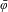$\bar{\unicode[STIX]{x1D711}}$ and consider the tilted Frenkel–Kontorova (FK) model:

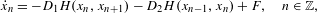$$\begin{eqnarray}{\dot{x}}_{n}=-D_{1}H(x_{n},x_{n+1})-D_{2}H(x_{n-1},x_{n})+F,\quad n\in \mathbb{Z},\end{eqnarray}$$
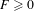where $F\geq 0$ is the driving force. The depinning force is the critical value 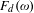$F_{d}(\unicode[STIX]{x1D714})$ depending on the mean spacing $\unicode[STIX]{x1D714}$ of particles, above which the tilted FK model is sliding, and below which the particles are pinned. We prove that there exists an invariant circle with irrational rotation number $\unicode[STIX]{x1D714}$ for 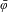$\bar{\unicode[STIX]{x1D711}}$ if and only if 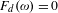$F_{d}(\unicode[STIX]{x1D714})=0$. For rational $\unicode[STIX]{x1D714}$, 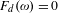$F_{d}(\unicode[STIX]{x1D714})=0$ is equivalent to the existence of an invariant circle on which 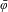$\bar{\unicode[STIX]{x1D711}}$ is topologically conjugate to the rational rotation with rotation number $\unicode[STIX]{x1D714}$. Such conclusions were claimed much earlier by Aubry et al. We also show that the depinning force 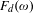$F_{d}(\unicode[STIX]{x1D714})$ is continuous at irrational $\unicode[STIX]{x1D714}$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 2 , April 2018 , pp. 761 - 787
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angenent, S.. The periodic points of an area-preserving twist map. Comm. Math. Phys. 115 (1988), 353–374.Google Scholar
Arnaud, M.-C.. A nondifferentiable essential irrational invariant curve for a C 1 symplectic twist map. J. Mod. Dyn. 5 (2011), 515–523.Google Scholar
Aubry, S. and Le Daeron, P. Y.. The discrete Frenkel–Kontorova model and its extensions. Physica D 8 (1983), 381–422.Google Scholar
Baesens, C. and MacKay, R. S.. Gradient dynamics of tilted Frenkel–Kontorova models. Nonlinearity 11 (1998), 949–964.Google Scholar
Bangert, V.. Mather sets for twist maps and geodesics on tori. Dynamics Reported. Vol. 1. Eds. Kirchgraber, U. and Walther, H. O.. Wiley, New York, 1988, pp. 1–56.Google Scholar
Bessi, U.. Many solutions of elliptic problems on ℝ n of irrational slope. Comm. Partial Differential Equations 30 (2005), 1773–1804.Google Scholar
Bessi, U. and Massart, D.. Mañé’s conjectures in codimension 1. Comm. Pure Appl. Math. 64 (2011), 1008–1027.Google Scholar
Birkhoff, G. D.. Surface transformations and their dynamical applications. Acta Math. 43 (1922), 1–119.Google Scholar
Braun, O. M. and Kivshar, Y. S.. The Frenkel–Kontorova Model, Concepts, Methods, and Applications. Springer, Berlin, 2004.Google Scholar
Calleja, R. and de la Llave, R.. A numerically accessible criterion for the breakdown of quasi-periodic solutions and its rigorous justification. Nonlinearity 23 (2010), 2029–2058.Google Scholar
Coppersmith, S. N. and Fisher, D. S.. Pinning transition of the discrete sine-Gordon equation. Phys. Rev. B 28 (1983), 2566–2581.Google Scholar
Coppersmith, S. N. and Fisher, D. S.. Threshold behavior of a driven incommensurate harmonic chain. Phys. Rev. A 38 (1988), 6338–6350.Google Scholar
de la Llave, R. and Valdinoci, E.. Multiplicity results for interfaces of Ginzburg–Landau–Allen–Cahn equations in periodic media. Adv. Math. 215 (2007), 379–426.Google Scholar
de la Llave, R. and Valdinoci, E.. Critical points inside the gaps of ground state laminations for some models in statistical mechanics. J. Stat. Phys. 129 (2007), 81–119.Google Scholar
de la Llave, R. and Valdinoci, E.. Ground states and critical points for Aubry–Mather theory in statistical mechanics. J. Nonlinear Sci. 20 (2010), 153–218.Google Scholar
Filip, A.-M. and Venakides, S.. Existence and modulation of traveling waves in particle chains. Comm. Pure Appl. Math. 51 (1999), 693–735.Google Scholar
Floría, L. M. and Mazo, J. J.. Dissipative dynamics of the Frenkel–Kontorova model. Adv. Phys. 45 (1996), 505–598.Google Scholar
Golé, C.. A new proof of the Aubry–Mather’s theorem. Math. Z. 210 (1992), 441–448.Google Scholar
Golé, C.. Ghost circles for twist maps. J. Differential Equations 97 (1992), 140–173.CrossRefGoogle Scholar
Golé, C.. Symplectic Twist Maps: Global Variational Techniques. World Scientific, Singapore, 2001.Google Scholar
Herman, M. R.. Sur les courbes invariantes par les difféomorphismes de l’anneau. Astérisque 1 (1983), 103–104.Google Scholar
Katok, A.. Some remarks on the Birkhoff and Mather twist theorems. Ergod. Th. & Dynam. Sys. 2 (1982), 183–194.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, New York, 1995.Google Scholar
Le Calvez, P.. Décomposition des difféomorphismes du tore en applications déviant la verticale. Mém. Soc. Math. Fr. (N.S.) 79 (1999), 3–148.Google Scholar
MacKay, R. S.. Scaling exponents at the transition by breaking of analyticity for incommensurate structures. Physica D 50 (1991), 71–79.Google Scholar
MacKay, R. S. and Percival, I. C.. Converse KAM: theory and practice. Comm. Math. Phys. 98 (1985), 469–512.Google Scholar
Marmi, S. and Yoccoz, J.-C.. Some open problems related to small divisors. Dynamical Systems and Small Divisors (Lecture Notes in Mathematics) . Eds. Marmi, S. and Yoccoz, J.-C.. Springer, Berlin, 2002, 1784.Google Scholar
Matano, H. and Rabinowitz, P. H.. On the necessity of gaps. J. Eur. Math. Soc. 8 (2006), 355–373.Google Scholar
Mather, J. N.. Existence of quasi-periodic orbits for twist homeomorphisms of the annulus. Topology 21 (1982), 457–467.Google Scholar
Mather, J. N.. A criterion for the non-existence of invariant circles. Publ. Math. Inst. Hautes Études Sci. 63 (1986), 153–204.Google Scholar
Mather, J. N.. Modulus of continuity for Peierls’s barrier. Periodic Solutions of Hamiltonian Systems and Related Topics. Ed. Rabinowitz, P. H. et al. . D. Reidel, Dordrecht, 1987, pp. 177–202.Google Scholar
Meiss, J. D.. Symplectic maps, variational principles, and transport. Rev. Mod. Phys. 64 (1992), 795–848.Google Scholar
Moser, J.. Stable and Random Motion in Dynamical Systems (Annals of Mathematical Studies, 77) . Princeton University Press, Princeton, NJ, 1973.Google Scholar
Moser, J.. Recent developments in the theory of Hamiltonian systems. SIAM Rev. 28 (1986), 459–485.Google Scholar
Mramor, B. and Rink, B.. Ghost circles in lattice Aubry–Mather theory. J. Differential Equations 252 (2012), 3163–3208.Google Scholar
Mramor, B. and Rink, B.. Continuity of the Peierls barrier and robustness of laminations. Ergod. Th. & Dynam. Sys. 35 (2015), 1263–1288.Google Scholar
Peyrard, M. and Aubry, S.. Critical behavior at the transition by breaking of analyticity in the discrete Frenkel–Kontorova model. J. Phys. C: Solid State Phys. 16 (1983), 1593–1608.Google Scholar
Qin, W.-X.. Dynamics of the Frenkel–Kontorova model with irrational mean spacing. Nonlinearity 23 (2010), 1873–1886.Google Scholar
Qin, W.-X.. Existence and modulation of uniform sliding states in driven and overdamped particle chains. Comm. Math. Phys. 311 (2012), 513–538.Google Scholar
Qin, W.-X.. Existence of dynamical hull functions with two variables for the ac-driven Frenkel–Kontorova model. J. Differential Equations 255 (2013), 3472–3490.Google Scholar
Smith, H. L.. Monotone Dynamical Systems. American Mathematical Society, Providence, RI, 1995.Google Scholar
Strunz, T. and Elmer, F.-J.. Driven Frenkel–Kontorova model: I. Uniform sliding states and dynamical domains of different particle densities. Phys. Rev. E 58 (1998), 1601–1611.Google Scholar