Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T23:53:27.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Imprimitivity theorems for weakly proper actions of locally compact groups

Published online by Cambridge University Press:  04 August 2014

ALCIDES BUSS  and
SIEGFRIED ECHTERHOFF
ALCIDES BUSS
Affiliation:
Departamento de Matemática, Universidade Federal de Santa Catarina, 88.040-900 Florianópolis-SC, Brazil email [email protected]
SIEGFRIED ECHTERHOFF
Affiliation:
Mathematisches Institut, University of Münster, Einsteinstr. 62, 48149 Münster, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In a recent paper the authors introduced universal and exotic generalized fixed-point algebras for weakly proper group actions on 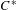$C^{\ast }$-algebras. Here we extend the notion of weakly proper actions to actions on Hilbert modules. As a result we obtain several imprimitivity theorems establishing important Morita equivalences between universal, reduced, or exotic crossed products and appropriate universal, reduced, or exotic fixed-point algebras, respectively. In particular, we obtain an exotic version of Green’s imprimitivity theorem and a very general version of the symmetric imprimitivity theorem by weakly proper actions of product groups 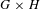$G\times H$. In addition, we study functorial properties of generalized fixed-point algebras for equivariant categories of 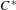$C^{\ast }$-algebras based on correspondences.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 8 , December 2015 , pp. 2412 - 2457
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

an Huef, A., Kaliszewski, S., Raeburn, I. and Williams, D. P.. Naturality of Rieffel’s Morita equivalence for proper actions. Algebr. Represent. Theory 14(3) (2011), 515–543.CrossRefGoogle Scholar
an Huef, A., Kaliszewski, S., Raeburn, I. and Williams, D. P.. Naturality of symmetric imprimitivity theorems. Proc. Amer. Math. Soc. 141(7) (2013), 2319–2327.CrossRefGoogle Scholar
an Huef, A., Raeburn, I. and Williams, D. P.. Functoriality of Rieffel’s generalised fixed-point algebras for proper actions. Superstrings, Geometry, Topology, and C ∗ -Algebras (Proceedings of Symposia in Pure Mathematics, 81). American Mathematical Society, Providence, RI, 2010, pp. 9–25.CrossRefGoogle Scholar
an Huef, A., Raeburn, I. and Williams, D. P.. A symmetric imprimitivity theorem for commuting proper actions. Canad. J. Math. 57(5) (2005), 983–1011.CrossRefGoogle Scholar
Baum, P., Connes, A. and Higson, N.. Classifying space for proper actions and K-theory of group C ∗ -algebras. C ∗ -Algebras: 1943–1993 (San Antonio, TX, 1993) (Contemporary Mathematics, 167). American Mathematical Society, Providence, RI, 1994, pp. 240–291.Google Scholar
Brown, N. P. and Guentner, E. P.. New C ∗ -completions of discrete groups and related spaces. Bull. Lond. Math. Soc. 45(6) (2013), 1181–1193.CrossRefGoogle Scholar
Buss, A. and Echterhoff, S.. Universal and exotic generalized fixed-point algebras for weakly proper actions and duality. eprint, 2013, arXiv:1304.5697.CrossRefGoogle Scholar
Combes, F.. Crossed products and Morita equivalence. Proc. Lond. Math. Soc. (3) 49(2) (1984), 289–306.CrossRefGoogle Scholar
Echterhoff, S. and Emerson, H.. Structure and K-theory of crossed products by proper actions. Expo. Math. 29(3) (2011), 300–344.CrossRefGoogle Scholar
Echterhoff, S., Kaliszewski, S., Quigg, J. and Raeburn, I.. Naturality and induced representations. Bull. Aust. Math. Soc. 61(3) (2000), 415–438.CrossRefGoogle Scholar
Echterhoff, S., Kaliszewski, S. P., Quigg, J. and Raeburn, I.. A categorical approach to imprimitivity theorems for C ∗ -dynamical systems. Mem. Amer. Math. Soc. 180(850) (2006), viii+169.Google Scholar
Echterhoff, S. and Raeburn, I.. Multipliers of imprimitivity bimodules and Morita equivalence of crossed products. Math. Scand. 76(2) (1995), 289–309.CrossRefGoogle Scholar
Exel, R.. Unconditional integrability for dual actions. Bol. Soc. Brasil. Mat. (N.S.) 30(1) (1999), 99–124.CrossRefGoogle Scholar
Green, P.. C ∗ -algebras of transformation groups with smooth orbit space. Pacific J. Math. 72(1) (1977), 71–97.CrossRefGoogle Scholar
Kaliszewski, S., Landstad, M. B. and Quigg, J.. Exotic group C∗ -algebras in noncommutative duality. New York J. Math. 19 (2013), 689–711.Google Scholar
Kaliszewski, S. P., Muhly, P. S., Quigg, J. and Williams, D. P.. Fell bundles and imprimitivity theorems: towards a universal generalized fixed point algebra. eprint, 2012, arXiv:1206.6739.CrossRefGoogle Scholar
Kaliszewski, S. P., Quigg, J. and Raeburn, I.. Proper actions, fixed-point algebras and naturality in nonabelian duality. J. Funct. Anal. 254(12) (2008), 2949–2968.CrossRefGoogle Scholar
Kasparov, G. G.. Equivariant KK-theory and the Novikov conjecture. Invent. Math. 91(1) (1988), 147–201.CrossRefGoogle Scholar
Kasparov, G. G. and Skandalis, G.. Groups acting properly on ‘bolic’ spaces and the Novikov conjecture. Ann. of Math. (2) 158(1) (2003), 165–206.CrossRefGoogle Scholar
Lance, E. C.. Hilbert C ∗ -modules: A Toolkit for Operator Algebraists (London Mathematical Society Lecture Note Series, 210). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Marelli, D. and Raeburn, I.. Proper actions which are not saturated. Proc. Amer. Math. Soc. 137(7) (2009), 2273–2283.CrossRefGoogle Scholar
Meyer, R.. Generalized fixed point algebras and square-integrable groups actions. J. Funct. Anal. 186(1) (2001), 167–195.CrossRefGoogle Scholar
Paul, B., Eric, G. and Rufus, W.. Expanders, exact crossed products, and the Baum–Connes conjecture. eprint, 2013, arXiv:1311.2343.Google Scholar
Quigg, J. C. and Spielberg, J.. Regularity and hyporegularity in C ∗ -dynamical systems. Houston J. Math. 18(1) (1992), 139–152.Google Scholar
Raeburn, I.. Induced C ∗ -algebras and a symmetric imprimitivity theorem. Math. Ann. 280(3) (1988), 369–387.CrossRefGoogle Scholar
Raeburn, I. and Williams, D. P.. Morita Equivalence and Continuous-Trace C ∗ -algebras (Mathematical Surveys and Monographs, 60). American Mathematical Society, Providence, RI, 1998, p. xiv+327.CrossRefGoogle Scholar
Rieffel, M. A.. Applications of strong Morita equivalence to transformation group C ∗ -algebras. Operator Algebras and Applications, Part I (Kingston, Ontario, 1980) (Proceedings of Symposia in Pure Mathematics, 38). American Mathematical Society, Providence, RI, 1982, pp. 299–310.CrossRefGoogle Scholar
Rieffel, M. A.. Proper actions of groups on C ∗ -algebras. Mappings of Operator Algebras (Philadelphia, PA, 1988) (Progress in Mathematics, 84). Birkhäuser, Boston, 1990, pp. 141–182.Google Scholar
Rieffel, M. A.. Integrable and proper actions on C ∗ -algebras, and square-integrable representations of groups. Expo. Math. 22(1) (2004), 1–53.CrossRefGoogle Scholar
Tu, J.-L.. La conjecture de Baum–Connes pour les feuilletages moyennables. K-Theory 17(3) (1999), 215–264.CrossRefGoogle Scholar
Williams, D. P.. Crossed Products of C ∗ -Algebras (Mathematical Surveys and Monographs, 134). American Mathematical Society, Providence, RI, 2007.CrossRefGoogle Scholar