Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T05:11:56.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperconvex representations and exponential growth

Published online by Cambridge University Press:  25 January 2013

A. SAMBARINO
A. SAMBARINO*
Affiliation:
Département de Mathématiques, Université Paris Sud, F-91405 Orsay, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

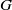Let $G$ be a real algebraic semi-simple Lie group and 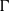$\Gamma $ be the fundamental group of a closed negatively curved manifold. In this article we study the limit cone, introduced by Benoist [Propriétés asymptotiques des groupes linéaires. Geom. Funct. Anal. 7(1) (1997), 1–47], and the growth indicator function, introduced by Quint [Divergence exponentielle des sous-groupes discrets en rang supérieur. Comment. Math. Helv. 77 (2002), 503–608], for a class of representations 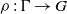$\rho : \Gamma \rightarrow G$ admitting an equivariant map from 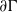$\partial \Gamma $ to the Furstenberg boundary of the symmetric space of 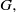$G, $ together with a transversality condition. We then study how these objects vary with the representation.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 3 , June 2014 , pp. 986 - 1010
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramov, L. M.. On the entropy of a flow. Dokl. Akad. Nauk SSSR 128 (1959), 873–875.Google Scholar
Akerkar, R.. Nonlinear Functional Analysis. Narosa Publishing House, 1999.Google Scholar
Barreira, L. and Pesin, Ya.. Lectures on Lyapunov exponents and smooth ergodic theory. Smooth Ergodic Theory and its Applications (Seattle, 1999) (Proc. Symp. in Pure Mathematics). American Mathematical Society, Providence, RI, 2000.Google Scholar
Benoist, Y.. Propriétés asymptotiques des groupes linéaires. Geom. Funct. Anal. 7 (1) (1997), 1–47.CrossRefGoogle Scholar
Benoist, Y.. Propriétés asymptotiques des groupes linéaires II. Adv. Stud. Pure Math. 26 (2000), 33–44.Google Scholar
Benoist, Y.. Convexes divisibles I. Algebraic Groups and Arithmetic. Tata Institute of Fundamental Research, 2004, pp. 339–374.Google Scholar
Bhatia, R. and Parthasarathy, K. R.. Lecture on Functional Analysis. MacMillan, Delhi, 1977.Google Scholar
Bowen, R.. Periodic orbits of hyperbolic flows. Amer. J. Math. 94 (1972), 1–30.CrossRefGoogle Scholar
Bowen, R.. Symbolic dynamics for hyperbolic flows. Amer. J. Math. 95 (1973), 429–460.Google Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of axiom A flows. Invent. Math. 29 (1975), 181–202.Google Scholar
Guichard, O. and Wienhard, A.. Anosov representations: domains of discontinuity and applications. Invent. Math. 190 (2012), 357–438.Google Scholar
Labourie, F.. Anosov flows, surface groups and curves in projective space. Invent. Math. 165 (2006), 51–114.Google Scholar
Ledrappier, F.. Structure au bord des variétés à courbure négative. Sémin. Théor. Spectr. Géom. 71 (1994–1995), 97–122.Google Scholar
Livšic, A. N.. Cohomology of dynamical systems. Math. USSR Izv. 6 (1972), 1278–1301.Google Scholar
Margulis, G.. Applications of ergodic theory to the investigation of manifolds with negative curvature. Funct. Anal. Appl. 3 (1969), 335–336.Google Scholar
Patterson, S.-J.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.Google Scholar
Pollicott, M. and Sharp, R.. Length asymptotics in higher Teichmüller theory. Preprint, 2012.Google Scholar
Quint, J.-F.. Divergence exponentielle des sous-groupes discrets en rang supérieur. Comment. Math. Helv. 77 (2002), 503–608.Google Scholar
Quint, J.-F.. Mesures de Patterson–Sullivan en rang supérieur. Geom. Funct. Anal. 12 (2002), 776–809.Google Scholar
Quint, J.-F.. L’indicateur de croissance des groupes de Schottky. Ergod. Th. & Dynam. Sys. 23 (2003), 249–272.CrossRefGoogle Scholar
Ratner, M.. The central limit theorem for geodesic flows on $n$-manifolds of negative curvature. Israel J. Math. 16 (1973), 181–197.Google Scholar
Ruelle, D.. Thermodynamic Formalism. Addison-Wesley, London, 1978.Google Scholar
Sambarino, A.. Quantitative properties of convex representations. Comm. Math. Helv., to appear, arXiv:1104.4705v1.Google Scholar
Shub, M.. Global Stability of Dynamical Systems. Springer, New York, 1987.Google Scholar
Sullivan, D.. The density at infinity of a discrete group of hyperbolic motions. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 171–202.CrossRefGoogle Scholar
Thirion, X.. Propriétés de mélange du flot des chambres de Weyl des groupes de Ping-Pong (Bulletin de la SMF, 137). Société mathématique de France, 2009, pp. 387–421.Google Scholar
Tits, J.. Représentations linéaires irréductibles d’un groupe réductif sur un corps quelconqe. J. Reine Angew. Math. 247 (1971), 196–220.Google Scholar
Yue, C.. The ergodic theory of discrete isometry groups on manifolds of variable negative curvature. Trans. Amer. Math. Soc. 348 (12) (1996), 4965–5005.Google Scholar