Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:12:08.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperbolicity versus weak periodic orbits inside homoclinic classes

Published online by Cambridge University Press:  14 March 2017

XIAODONG WANG
XIAODONG WANG*
Affiliation:
School of Mathematical Sciences, Shanghai Jiao Tong University, Shanghai, 200240, China School of Mathematical Sciences, Peking University, Beijing, 100871, China Laboratoire de Mathématiques d’Orsay, Université Paris-Sud 11, Orsay, 91405, France email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that, for 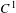$C^{1}$-generic diffeomorphisms, if the periodic orbits contained in a homoclinic class 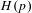$H(p)$ have all their Lyapunov exponents bounded away from zero, then 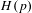$H(p)$ must be (uniformly) hyperbolic. This is in the spirit of the works on the stability conjecture, but with a significant difference that the homoclinic class 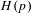$H(p)$ is not known isolated in advance, hence the ‘weak’ periodic orbits created by perturbations near the homoclinic class have to be guaranteed strictly inside the homoclinic class. In this sense the problem is of an ‘intrinsic’ nature, and the classical proof of the stability conjecture does not work. In particular, we construct in the proof several perturbations which are not simple applications of the connecting lemmas.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 6 , September 2018 , pp. 2345 - 2400
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F., Bonatti, C., Crovisier, S., Díaz, L. and Wen, L.. Periodic points and homoclinic classes. Ergod. Th. & Dynam. Sys. 27 (2007), 1–22.Google Scholar
Abdenur, F., Bonatti, C. and Díaz, L.. Nonwandering sets with non empy interior. Nonlinearity 17 (2004), 175–191.Google Scholar
Aoki, N.. The set of Axiom A diffeomorphisms with no cycles. Bol. Soc. Brasil Mat. 23 (1992), 21–65.Google Scholar
Arbieto, A., Carvalho, B., Cordeiro, W. and Obata, D. J.. On bi-Lyapunov stable homoclinic classes. Bull. Braz. Math. Soc. (N.S.) 44 (2013), 105–127.Google Scholar
Arnaud, M.-C.. Le ‘closing lemma’ en topologie C 1 . Mém. Soc. Math. Fr. (N.S.) 74 (1998), 120pp.Google Scholar
Arnaud, M.-C.. Création de connexions en topologie C 1 . Ergod. Th. & Dynam. Sys. 21 (2001), 339–381.Google Scholar
Bonatti, C.. Towards a global view of dynamical systems, for the C 1 -topology. Ergod. Th. & Dynam. Sys. 31 (2011), 959–993.Google Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158 (2004), 33–104.Google Scholar
Bonatti, C., Crovisier, S., Díaz, L. and Gourmelon, N.. Internal perturbations of homoclinic classes: non-domination, cycles, and self-replication. Ergod. Th. & Dynam. Sys. 33 (2013), 739–776.Google Scholar
Bonatti, C. and Díaz, L.. On maximal transitive sets of generic diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 96 (2003), 171–197.Google Scholar
Bonatti, C. and Díaz, L.. Robust heterodimensional cycles and C 1 -generic dynamics. J. Inst. Math. Jussieu 7 (2008), 469–525.Google Scholar
Bonatti, C., Díaz, L. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity. A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102) . Springer, New York, 2005, Mathematical Physics, III.Google Scholar
Bonatti, C., Gan, S. and Yang, D.. On the hyperbolicity of homoclinic classes. Discrete Contin. Dyn. Syst. 25 (2009), 1143–1162.Google Scholar
Bonatti, C. and Shinohara, K.. Volume hyperbolicity and wildness. Ergod. Th. & Dynam. Sys. to appear.Google Scholar
Cao, Y., Luzzatto, S. and Rios, I.. Some non-hyperbolic systems with strictly non-zero Lyapunov exponents for all invariant measures: horseshoes with internal tangencies. Discrete Contin. Dyn. Syst. 15(1) (2006), 61–71.Google Scholar
Conley, C.. Isolated Invariant Sets and the Morse Index (CBMS Regional Conference Series in Mathematics, 38) . American Mathematical Society, Providence, RI, 1978.Google Scholar
Crovisier, S.. Saddle-node bifurcations for hyperbolic sets. Ergod. Th. & Dynam. Sys. 22 (2002), 1079–1115.Google Scholar
Crovisier, S.. Periodic orbits and chain-transitive sets of C 1 -diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 104 (2006), 87–141.Google Scholar
Crovisier, S.. Partial hyperbolicity far from homoclinic bifurcations. Adv. Math. 226 (2011), 673–726.Google Scholar
Crovisier, S.. Perturbation de la dynamique de difféomorphismes en petite régularité. Astérisque 354 (2013), 164pp.Google Scholar
Crovisier, S.. Dynamics of C 1 -diffeomorphisms: global description and prospect of classification. Proceedings of the International Congress of Mathematicians. Vol. III. Kyung Moon, Seoul, 2014, pp. 571–595.Google Scholar
Crovisier, S. and Pujals, E.. Essential hyperbolicity and homoclinic bifurcations: a dichotomy phenomenon/mechanism for diffeomorphisms. Invent. Math. 201 (2015), 385–517.Google Scholar
Crovisier, S., Sambarino, M. and Yang, D.. Partial hyperbolicity and homoclinic tangencies. J. Eur. Math. Soc. (JEMS) 17 (2015), 1–49.Google Scholar
Díaz, L. and Gelfert, K.. Porcupine-like horseshoes: transitivity, Lyapunov spectrum, and phase transitions. Fund. Math. 216 (2012), 55–100.Google Scholar
Díaz, L., Horita, V., Rios, I. and Sambarino, M.. Destroying horseshoes via heterodimensional cycles: generating bifurcations inside homoclinic classes. Ergod. Th. & Dynam. Sys. 29 (2009), 433–474.Google Scholar
Franks, J.. Necessary conditions for stability of diffeomorphisms. Trans. Amer. Math. Soc. 158 (1971), 301–308.Google Scholar
Gan, S. and Wen, L.. Heteroclinic cycles and homoclinic closures for generic diffeomorphisms. J. Dynam. Differential Equations 15 (2003), 451–471.Google Scholar
Gan, S. and Yang, D.. Expansive homoclinic classes. Nonlinearity 22 (2009), 729–734.Google Scholar
Gourmelon, N.. Adapted metrics for dominated splittings. Ergod. Th. & Dynam. Sys. 27 (2007), 1839–1849.Google Scholar
Gourmelon, N.. A Frank’s lemma that preserves invariant manifolds. Ergod. Th. & Dynam. Sys. 36 (2016), 1167–1203.Google Scholar
Hayashi, S.. Connecting invariant manifolds and the solution of the C 1 -stability and 𝛺-stability conjectures for flows. Ann. of Math. (2) 145 (1997), 81–137.Google Scholar
Hayashi, S.. Diffeomorphisms in F1(M) satisfy Axiom A. Ergod. Th. & Dynam. Sys. 12 (1992), 233–253.Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583) . Springer, Berlin, 1977.Google Scholar
Liao, S.. On the stability conjecture. Chinese Ann. Math. 1 (1980), 9–30.Google Scholar
Liao, S.. Obstruction sets II. Acta Sci. Natur. Univ. Pekinensis 2 (1981), 1–36 (in Chinese).Google Scholar
Mañé, R.. An ergodic closing lemma. Ann. of Math. (2) 116 (1982), 503–540.Google Scholar
Mañé, R.. A proof of the C 1 stability conjecture. Publ. Math. Inst. Hautes Études Sci. 66 (1988), 161–210.Google Scholar
Palis, J.. On the C 1 𝛺-stability conjecture. Publ. Math. Inst. Hautes Études Sci. 66 (1988), 211–215.Google Scholar
Palis, J.. A global view of dynamics and a conjecture on the denseness of finitude of attractors. Astérisque 261 (2000), 335–347.Google Scholar
Pliss, V.. On a conjecture due to Smale. Differ. Uravn. 8 (1972), 262–268.Google Scholar
Potrie, R.. Generic bi-Lyapunov stable homoclinic classes. Nonlinearity 23 (2010), 1631–1649.Google Scholar
Pugh, C. and Robinson, C.. The C 1 closing lemma, including Hamiltonians. Ergod. Th. & Dynam. Sys. 3 (1983), 261–313.Google Scholar
Pujals, E. and Sambarino, M.. Homoclinic tangencies and hyperbolicity for suface diffeomorphisms. Ann. of Math. (2) 151 (2000), 961–1023.Google Scholar
Pujals, E. and Sambarino, M.. On the dynamics of dominated splitting. Ann. of Math. (2) 169 (2009), 675–740.Google Scholar
Rios, I.. Unfolding homoclinic tangencies inside horseshoes: hyperbolicity, fractal dimensions and persistent tangencies. Nonlinearity 14 (2001), 431–462.Google Scholar
Sambarino, M. and Vieitez, J.. On C 1 -persistently expansive homoclinic classes. Discrete Contin. Dyn. Syst. 14 (2006), 465–481.Google Scholar
Wen, L.. Homoclinic tangencies and dominated splittings. Nonlinearity 15 (2002), 1445–1469.Google Scholar
Wen, L.. A uniform C 1 connecting lemma. Discrete Contin. Dyn. Syst. 8 (2002), 257–265.Google Scholar
Wen, L.. The selecting lemma of Liao. Discrete Contin. Dyn. Syst. 20 (2008), 159–175.Google Scholar
Wen, L. and Xia, Z.. C 1 connecting lemmas. Trans. Amer. Math. Soc. 352 (2000), 5213–5230.Google Scholar
Wen, X.. Structurally stable homoclinic classes. Discrete Contin. Dyn. Syst. 36 (2016), 1693–1707.Google Scholar
Wen, X., Gan, S. and Wen, L.. C 1 -stably shadowable chain components are hyperbolic. J. Differential Equations 246 (2009), 340–357.Google Scholar
Wen, X. and Wen, L.. Codimension one structurally stable chain classes. Trans. Amer. Math. Soc. 368 (2016), 3849–3870.Google Scholar