No CrossRef data available.
Published online by Cambridge University Press: 17 June 2022
For a
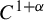 $C^{1+\alpha }$
diffeomorphism f of a compact smooth manifold, we give a necessary and sufficient condition that guarantees that if the set of hyperbolic Lyapunov–Perron regular points has positive volume, then f preserves a smooth measure. We use recent results on symbolic coding of
$C^{1+\alpha }$
diffeomorphism f of a compact smooth manifold, we give a necessary and sufficient condition that guarantees that if the set of hyperbolic Lyapunov–Perron regular points has positive volume, then f preserves a smooth measure. We use recent results on symbolic coding of
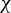 $\chi $
-non-uniformly hyperbolic sets and results concerning the existence of SRB measures for them.
$\chi $
-non-uniformly hyperbolic sets and results concerning the existence of SRB measures for them.