Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Duarte, Pedro
and
Klein, Silvius
2014.
Continuity of the Lyapunov Exponents for Quasiperiodic Cocycles.
Communications in Mathematical Physics,
Vol. 332,
Issue. 3,
p.
1113.
Rueß, Johannes
2016.
Continuity results and estimates for the Lyapunov exponent of Brownian motion in stationary potential.
Brazilian Journal of Probability and Statistics,
Vol. 30,
Issue. 3,
Duarte, Pedro
and
Klein, Silvius
2016.
Large deviation type estimates for iterates of linear cocycles.
Stochastics and Dynamics,
Vol. 16,
Issue. 03,
p.
1660010.
Wang, Yiqian
and
You, Jiangong
2018.
The Set of Smooth Quasi-periodic Schrödinger Cocycles with Positive Lyapunov Exponent is Not Open.
Communications in Mathematical Physics,
Vol. 362,
Issue. 3,
p.
801.
Jian, Wenwen
and
Shi, Yunfeng
2019.
Sharp Hölder Continuity of the Integrated Density of States for Extended Harper’s Model with a Liouville Frequency.
Acta Mathematica Scientia,
Vol. 39,
Issue. 5,
p.
1240.
Wang, Fengpeng
and
Damanik, David
2019.
Anderson localization for quasi-periodic CMV matrices and quantum walks.
Journal of Functional Analysis,
Vol. 276,
Issue. 6,
p.
1978.
Guo, Shuzheng
and
Piao, Daxiong
2020.
Lyapunov behavior and dynamical localization for quasi-periodic CMV matrices.
Linear Algebra and its Applications,
Vol. 606,
Issue. ,
p.
68.
Geng, Wenmeng
and
Tao, Kai
2021.
Lyapunov exponents of discrete quasi-periodic gevrey Schrödinger equations.
Discrete & Continuous Dynamical Systems - B,
Vol. 26,
Issue. 6,
p.
2977.
Cedzich, C.
and
Werner, A. H.
2021.
Anderson Localization for Electric Quantum Walks and Skew-Shift CMV Matrices.
Communications in Mathematical Physics,
Vol. 387,
Issue. 3,
p.
1257.
Zhao, Xin
2021.
Hölder continuity of absolutely continuous spectral measure for the extended HARPER’S model.
Nonlinearity,
Vol. 34,
Issue. 5,
p.
3356.
Ge, Lingrui
You, Jiangong
and
Zhao, Xin
2022.
Hölder Regularity of the Integrated Density of States for Quasi-periodic Long-range Operators on $$\ell ^2({\mathbb {Z}}^d)$$.
Communications in Mathematical Physics,
Vol. 392,
Issue. 2,
p.
347.
Tao, Kai
2022.
Strong Birkhoff ergodic theorem for subharmonic functions with irrational shift and its application to analytic quasi-periodic cocycles.
Discrete & Continuous Dynamical Systems,
Vol. 42,
Issue. 3,
p.
1495.
Han, Rui
and
Zhang, Shiwen
2022.
Large Deviation Estimates and Hölder Regularity of the Lyapunov Exponents for Quasi-periodic Schrödinger Cocycles.
International Mathematics Research Notices,
Vol. 2022,
Issue. 3,
p.
1666.
Zhang, Bei
2024.
The Hölder continuity of the Lyapunov exponent for a quasi-periodic Szegő cocycle.
Acta Mathematica Scientia,
Vol. 44,
Issue. 6,
p.
2099.
Liang, Jinhao
Wang, Yiqian
and
You, Jiangong
2024.
Hölder Continuity of Lyapunov Exponent for a Family of Smooth Schrödinger Cocycles.
Annales Henri Poincaré,
Vol. 25,
Issue. 2,
p.
1399.
Xu, Jiahao
2024.
A Generalization of the Avalanche Principle.
Frontiers of Mathematics,
Vol. 19,
Issue. 3,
p.
457.
Powell, M.
2024.
Pointwise modulus of continuity of the Lyapunov exponent and integrated density of states for analytic multi-frequency quasi-periodic M(2,C) cocycles.
Journal of Mathematical Physics,
Vol. 65,
Issue. 3,
Wang, Jing
2025.
Hölder Continuity of the Integrated Density of States and Lyapunov Exponent for Quasi-Periodic Schrödinger Operator with Liouvillean Frequency.
Annales Henri Poincaré,
Xu, Jiahao
Ge, Lingrui
and
Wang, Yiqian
2025.
The Precise Regularity of the Lyapunov Exponent for $$C^2$$ Cos-Type Quasiperiodic Schrödinger Cocycles with Large Couplings.
Communications in Mathematical Physics,
Vol. 406,
Issue. 4,
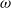 $\omega $ satisfies a strong Diophantine condition. In this paper, we give a refined large deviation theorem, which implies the Hölder continuity of the Lyapunov exponent for all Diophantine frequencies
$\omega $ satisfies a strong Diophantine condition. In this paper, we give a refined large deviation theorem, which implies the Hölder continuity of the Lyapunov exponent for all Diophantine frequencies 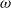 $\omega $, even for weak Liouville
$\omega $, even for weak Liouville 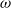 $\omega $, which improves the result of Goldshtein and Schlag.
$\omega $, which improves the result of Goldshtein and Schlag.

