Article contents
Helicity of vector fields preserving a regular contact form and topologically conjugate smooth dynamical systems
Published online by Cambridge University Press: 29 June 2012
Abstract
We compute the helicity of a vector field preserving a regular contact form on a closed three-dimensional manifold, and improve results of Gambaudo and Ghys [Enlacements asymptotiques. Topology 36(6) (1997), 1355–1379] relating the helicity of the suspension of a surface isotopy to the Calabi invariant of the isotopy. Based on these results, we provide positive answers to two questions posed by Arnold in [The asymptotic Hopf invariant and its applications. Selecta Math. Soviet. 5(4) (1986), 327–345]. In the presence of a regular contact form that is also preserved, the helicity extends to an invariant of an isotopy of volume-preserving homeomorphisms, and is invariant under conjugation by volume-preserving homeomorphisms. A similar statement also holds for suspensions of surface isotopies and surface diffeomorphisms. This requires the techniques of topological Hamiltonian and contact dynamics developed by Banyaga and Spaeth [On the uniqueness of generating Hamiltonians for topological strictly contact isotopies. Preprint, 2012], Buhovsky and Seyfaddini [Uniqueness of generating Hamiltonians for continuous Hamiltonian flows. J. Symplectic Geom. to appear, arXiv:1003.2612v2], Müller [The group of Hamiltonian homeomorphisms in the 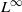 $L^\infty $-norm. J. Korean Math. Soc.45(6) (2008), 1769–1784], Müller and Oh [The group of Hamiltonian homeomorphisms and
$L^\infty $-norm. J. Korean Math. Soc.45(6) (2008), 1769–1784], Müller and Oh [The group of Hamiltonian homeomorphisms and 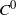 $C^0$-symplectic topology. J. Symplectic Geom. 5(2) (2007), 167–219], Müller and Spaeth [Topological contact dynamics I: symplectization and applications of the energy-capacity inequality. Preprint, 2011, arXiv:1110.6705v2] and Viterbo [On the uniqueness of generating Hamiltonian for continuous limits of Hamiltonians flows. Int. Math. Res. Not. (2006), 34028; Erratum, Int. Math. Res. Not. (2006), 38748]. Moreover, we generalize an example of Furstenberg [Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601] on topologically conjugate but not
$C^0$-symplectic topology. J. Symplectic Geom. 5(2) (2007), 167–219], Müller and Spaeth [Topological contact dynamics I: symplectization and applications of the energy-capacity inequality. Preprint, 2011, arXiv:1110.6705v2] and Viterbo [On the uniqueness of generating Hamiltonian for continuous limits of Hamiltonians flows. Int. Math. Res. Not. (2006), 34028; Erratum, Int. Math. Res. Not. (2006), 38748]. Moreover, we generalize an example of Furstenberg [Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601] on topologically conjugate but not 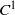 $C^1$-conjugate area-preserving diffeomorphisms of the two-torus to trivial
$C^1$-conjugate area-preserving diffeomorphisms of the two-torus to trivial 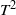 $T^2$-bundles, and construct examples of Hamiltonian and contact vector fields that are topologically conjugate but not
$T^2$-bundles, and construct examples of Hamiltonian and contact vector fields that are topologically conjugate but not  $C^1$-conjugate. Higher-dimensional helicities are considered briefly at the end of the paper.
$C^1$-conjugate. Higher-dimensional helicities are considered briefly at the end of the paper.
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 2
- Cited by


