Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-19T09:29:09.801Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hausdorff dimension of certain solenoids

Published online by Cambridge University Press:  19 September 2008

H. G. Bothe
H. G. Bothe
Affiliation:
Weierstrass Institute for Applied Analysis and Stochastics, Mohrenstr. 39, D-10117 Berlin, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

For the solid torus V = S1 × 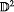and a C1 embedding f: V → V given by 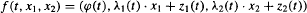with dϕ/dt > 1, 0 < λi(t) < 1 the attractor Λ = ∩i = 0∞fi(V) is a solenoid, and for each disk D(t) = {t} × 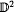(t ∈ S1) the intersection Λ(t) = Λ ∩ D(t) is a Cantor set. It is the aim of the paper to find conditions under which the Hausdorff dimension of Λ(t) is independent of t and determined by where the real numbers pi are characterized by the condition that the pressure of the function log 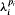: S1 → ℝ with respect to the expanding mapping ϕ: S1 → S1 becomes zero. (There are two further characterizations of these numbers.)

It is proved that (0.1) holds provided λ1, λ2 are sufficiently small and Λ satisfies a condition called intrinsic transverseness. Then it is shown that in the C1 space of all embeddings f with sup λi > Θ−2 (Θ the mapping degree of ϕ: S1 → S1) all those f which have an intrinsically transverse attractor Λ form an open and dense subset.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 15 , Issue 3 , June 1995 , pp. 449 - 474
Copyright
Copyright © Cambridge University Press 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bothe, H. G.. Expanding attractors with stable foliations of class C 0. Ergodic Theory and Related Topics III, Proc. Conf. Güstrow 1990. Springer Lecture Notes in Mathematics 1514. Springer: Berlin, 1992. pp. 36–61.Google Scholar
[2]Bowen, R.. Equilibrium states and the ergodic theory of Anosov diffeomorphisms. Springer Lecture Notes in Mathematics 470. Springer: Berlin, 1975.Google Scholar
[3]Falconer, K. J.. The geometry of fractal sets. Cambridge Tracts in Mathematics 85. Cambridge University Press: Cambridge, 1985.Google Scholar
[4]Falconer, K. J.The Hausdorff dimension of some fractals and attractors of overlapping construction. J. Stat. Phys. 47 (1987), 123–132.CrossRefGoogle Scholar
[5]McCluskey, H. and Manning, A.. Hausdorff dimension for horseshoes. Ergod. Th. & Dynam. Sys. 3 (1983), 251–260.CrossRefGoogle Scholar
[6]Robinson, C. and Williams, R.. Classification of expanding attractors: An example. Topology 15 (1976), 321–323.CrossRefGoogle Scholar
[7]Ruelle, D.. Thettnodynamic formalism. Encyclopedia of Mathematics and its Applications. Vol. 5. Addison-Wesley: Reading, MA, 1978.Google Scholar
[8]Schaefer, H. H.. Topological vector spaces. Graduate Texts in Mathematics 3. Springer: New York—Heidelberg—Berlin, 1971.Google Scholar
[9]Shub, M.. Global Stability of Dynamical Systems. Springer: Berlin, 1987.CrossRefGoogle Scholar
[10]Simon, K.. Hausdorff dimension for non-invertible maps. Ergod. Th. & Dynam. Sys.. 13 (1993), 199–212.CrossRefGoogle Scholar
[11]Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc.. 73 (1967), 747–817.CrossRefGoogle Scholar
[12]Williams, R.. Expanding attractors. Publ. Math. IHES 43 (1974), 169–203.CrossRefGoogle Scholar