Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T00:58:47.782Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups acting freely on R-trees

Published online by Cambridge University Press:  19 September 2008

John W. Morgan  and
Richard K. Skora
John W. Morgan
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA
Richard K. Skora
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the question of which groups act freely on R-trees. The paper has two parts. The first part concerns groups which contain a non-cyclic, abelian subgroup. The following is the main result in this case.

Let the finitely presented group G act freely on an R-tree. If A is a non-cyclic, abelian subgroup of G, then A is contained in an abelian subgroup A′ which is a free factor of G.

The second part of the paper concerns groups whch split as an HNN-extension along an infinite cyclic group. Here is one formulation of our main result in that case.

Let the finitely presented group G act freely on an R-tree. If G has an HNN-decomposition

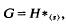
where (s) is infinite cyclic, then there is a subgroup H′ ⊂ H such that either

(a) 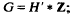; or

(b) 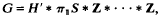, where S is a closed surface of non-positive Euler characteristic.

A slightly different, more precise result is also given.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 11 , Issue 4 , December 1991 , pp. 737 - 756
Copyright
Copyright © Cambridge University Press 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A-B]Alperin, R. & Bass, H.. Length functions of group actions on A-Trees. In: Gersten, S. M. et al. , eds, Combinatorial Group Theory and Topology. Annals of Math Studies 111, Princeton University Press, Princeton (1987), pp. 265–378.CrossRefGoogle Scholar
[Cu-Mo]Culler, M. & Morgan, J. W.. Group actions on R-trees. Proc. Lond. Math. Soc. 55 (1987), 571–604.CrossRefGoogle Scholar
[G-S]Gillet, H. & Shalen, P. B.. Dendrology of groups in low Q-ranks. J. Diff. Geo. 32 (1990), 605–712.Google Scholar
[Ly-Sh]Lyndon, R. C. & Shupp, P.. Combinatorial Group Theory (Ergebnisse der Mathematik und ihrer Grenzgebiete), Vol 89, Berlin-Heidelberg-New York, Springer, 1977.Google Scholar
[Mo]Morgan, J. W.. Ergodic theory and free actions on trees. Invent. Math. 94 (1988), 605–622.CrossRefGoogle Scholar
[Mo-Sh1]Morgan, J. W. & Shalen, P. B.. Degenerations of hyperbolic structures, I: Valuations, trees and surfaces. Ann. Math. 120 (1984), 401–476.CrossRefGoogle Scholar
[Mo-Sh2]Morgan, J. W. & Shalen, P. B.. Degenerations of hyperbolic structures, II: measured laminations in 3-manifolds. Ann. Math. 127 (1988) 403–456.Google Scholar
[Mo-Sh3]Morgan, J. W. & Shalen, P. B.. Degenerations of hyperbolic structures, III: actions of 3-manifold groups on trees and Thurston's compactness theorem. Ann. Math. 12 (1988) 457–519.Google Scholar
[Ser]Serre, J. -P.. Trees. Springer-Verlag, New York, 1980.CrossRefGoogle Scholar
[Sha]Shalen, P. B.. Dendrology of Groups: An Introduction. In: Gersten, S. M., ed., Essays in Group Theory. Mathematical Sciences Research Institute Publications, 8, Springer-Verlag, New York.Google Scholar
[Sk]Skora, R. K.. Splittings of surfaces. Bull. Amer. Math. Soc. 23 (1990), 85–90.Google Scholar