Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T01:26:51.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Ground states and zero-temperature measures at the boundary of rotation sets

Published online by Cambridge University Press:  02 May 2017

TAMARA KUCHERENKO  and
CHRISTIAN WOLF
TAMARA KUCHERENKO
Affiliation:
Department of Mathematics, The City College of New York, New York, NY 10031, USA email [email protected], [email protected]
CHRISTIAN WOLF
Affiliation:
Department of Mathematics, The City College of New York, New York, NY 10031, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a continuous dynamical system 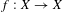$f:X\rightarrow X$ on a compact metric space 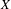$X$ equipped with an 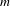$m$-dimensional continuous potential 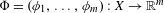$\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{m}):X\rightarrow \mathbb{R}^{m}$. We study the set of ground states 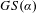$GS(\unicode[STIX]{x1D6FC})$ of the potential 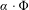$\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D6F7}$ as a function of the direction vector 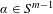$\unicode[STIX]{x1D6FC}\in S^{m-1}$. We show that the structure of the ground state sets is naturally related to the geometry of the generalized rotation set of 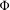$\unicode[STIX]{x1D6F7}$. In particular, for each $\unicode[STIX]{x1D6FC}$ the set of rotation vectors of 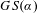$GS(\unicode[STIX]{x1D6FC})$ forms a non-empty, compact and connected subset of a face 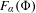$F_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6F7})$ of the rotation set associated with $\unicode[STIX]{x1D6FC}$. Moreover, every ground state maximizes entropy among all invariant measures with rotation vectors in 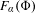$F_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6F7})$. We further establish the occurrence of several quite unexpected phenomena. Namely, we construct for any 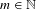$m\in \mathbb{N}$ examples with an exposed boundary point (that is, 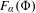$F_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6F7})$ being a singleton) without a unique ground state. Further, we establish the possibility of a line segment face 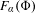$F_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6F7})$ with a unique but non-ergodic ground state. Finally, we establish the possibility that the set of rotation vectors of 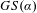$GS(\unicode[STIX]{x1D6FC})$ is a non-trivial line segment.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 1 , January 2019 , pp. 201 - 224
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bissacot, R., Garibaldi, E. and Thieullen, P.. Zero-temperature phase diagram for double-well type potentials in the summable variation class. Ergod. Th. & Dynam. Sys. (2016), 1–23. Published online: 19 September.Google Scholar
Bousch, T.. Le poisson n’a pas d’aretes. Ann. Inst. Henri. Poincaré Probab. Stat. 36 (2000), 489–508.Google Scholar
Brémont, J.. Gibbs measures at temperature zero. Nonlinearity 16 (2003), 419–426.Google Scholar
Chazottes, J. R., Gambaudo, J. M. and Ugalde, E.. Zero-temperature limit of one-dimensional Gibbs states via renormalization: the case of locally constant potentials. Ergod. Th. & Dynam. Sys. 31 (2011), 1109–1161.Google Scholar
Chazottes, J. R. and Hochman, M.. On the zero-temperature limit of Gibbs states. Comm. Math. Phys. 297(1) (2010), 265–281.Google Scholar
Climenhaga, V., Fisher, T. and Thompson, D.. Unique equilibrium states for Bonatti–Viana diffeomorphisms. Preprint.Google Scholar
Climenhaga, V. and Pesin, Ya.. Building thermodynamics for non-uniformly hyperbolic maps. Arnold Math. J. to appear.Google Scholar
Climenhaga, V. and Thompson, D.. Intrinsic ergodicity beyond specification: -shifts, S-gap shifts, and their factors. Israel J. Math. 192 (2012), 785–817.Google Scholar
Climenhaga, V. and Thompson, D.. Equilibrium states beyond specification and the Bowen property. J. Lond. Math. Soc. (2) 87 (2013), 401–427.Google Scholar
Climenhaga, V. and Thompson, D.. Unique equilibrium states for flows and homeomorphisms with non-uniform structure. Adv. Math. 303 (2016), 745–799.Google Scholar
Contreras, G.. Ground states are generically a periodic orbit. Invent. Math. 205 (2016), 383–412.Google Scholar
Contreras, G., Lopes, A. O. and Thieullen, P.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 21 (2001), 1379–1409.Google Scholar
Coronel, D. and Rivera-Letelier, J.. Sensitive dependence of Gibbs measures at low temperatures. J. Stat. Phys. 160 (2015), 1658–1683.Google Scholar
Garibaldi, E. and Lopes, A. O.. Functions for relative maximization. Dyn. Syst. 22 (2007), 511–528.Google Scholar
Geller, W. and Misiurewicz, M.. Rotation and entropy. Trans. Amer. Math. Soc. 351 (1999), 2927–2948.Google Scholar
Giulietti, P., Kloeckner, B., Lopes, A. O. and Marcon, D.. The calculus of thermodynamic formalism. J. Eur. Math. Soc. to appear.Google Scholar
Grünbaum, B.. Convex Polytopes (Pure and Applied Mathematics, XVI) . Interscience, John Wiley and Sons, New York, 1967.Google Scholar
Jenkinson, O.. Rotation, entropy, and equilibrium states. Trans. Amer. Math. Soc. 353 (2001), 3713–3739.Google Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. 15 (2006), 197–224.Google Scholar
Jenkinson, O, Mauldin, D. and Urbanski, M.. Zero temperature limits of Gibbs-equilibrium states for countable alphabet subshifts of finite type. J. Stat. Phys. 119 (2005), 765–776.Google Scholar
Kempton, T.. Zero temperature limits of Gibbs equilibrium states for countable Markov shifts. J. Stat. Phys. 143 (2011), 795–806.Google Scholar
Kucherenko, T. and Wolf, C.. The geometry and entropy of rotation sets. Israel J. Math. 1999 (2014), 791–829.Google Scholar
Kucherenko, T. and Wolf, C.. Localized pressure and equilibrium states. J. Stat. Phys. 160 (2015), 1529–1544.Google Scholar
Kucherenko, T. and Wolf, C.. Entropy and rotation sets: A toymodel approach. Commun. Contemp. Math. 18 (2016), 23 pp.Google Scholar
Leplaideur, R.. A dynamical proof for the convergence of Gibbs measures at temperature zero. Nonlinearity 18 (2005), 2847–2880.Google Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets and ergodic measures for torus homeomorphisms. Fund. Math. 137 (1991), 45–52.Google Scholar
Morris, I.. Maximizing measures of generic Hölder functions have zero entropy. Nonlinearity 21 (2008), 993–1000.Google Scholar
Parthasarathy, K. R.. On the category of ergodic measures. Illinois J. Math. 5 (1961), 648–656.Google Scholar
Van Enter, A., Fernández, R. and Sokal, A.. Regularity properties and pathologies of position-space renormalization-group transformations: scope and limitations of Gibbsian theory. J. Stat. Phys. 72 (1993), 879–1167.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar
Ziemian, K.. Rotation sets for subshifts of finite type. Fund. Math. 146 (1995), 189–201.Google Scholar