Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T08:09:26.729Z Has data issue: false hasContentIssue false
  • English
  • Français

A good universal weight for nonconventional ergodic averages in norm

Published online by Cambridge University Press:  28 December 2015

IDRIS ASSANI  and
RYO MOORE
IDRIS ASSANI
Affiliation:
Department of Mathematics, The University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA email [email protected], [email protected]
RYO MOORE
Affiliation:
Department of Mathematics, The University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We will show that the sequence appearing in the double recurrence theorem is a good universal weight for the Furstenberg averages. That is, given a system 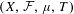$(X,{\mathcal{F}},\unicode[STIX]{x1D707},T)$ and bounded functions 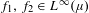$f_{1},f_{2}\in L^{\infty }(\unicode[STIX]{x1D707})$, there exists a set of full-measure 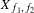$X_{f_{1},f_{2}}$ in $X$ that is independent of integers $a$ and 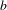$b$ and a positive integer 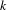$k$ such that, for all 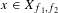$x\in X_{f_{1},f_{2}}$, for every other measure-preserving system 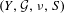$(Y,{\mathcal{G}},\unicode[STIX]{x1D708},S)$ and for each bounded and measurable function 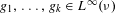$g_{1},\ldots ,g_{k}\in L^{\infty }(\unicode[STIX]{x1D708})$, the averages

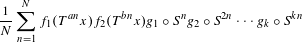$$\begin{eqnarray}\frac{1}{N}\mathop{\sum }_{n=1}^{N}f_{1}(T^{an}x)f_{2}(T^{bn}x)g_{1}\circ S^{n}g_{2}\circ S^{2n}\cdots g_{k}\circ S^{kn}\end{eqnarray}$$
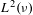converge in $L^{2}(\unicode[STIX]{x1D708})$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1009 - 1025
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assani, I.. Multiple recurrence and almost sure convergence for weakly mixing dynamical systems. Israel J. Math. 103 (1998), 111–124.CrossRefGoogle Scholar
Assani, I.. Multiple return times theorems for weakly mixing systems. Ann. Inst. Henri Poincaré Probab. Stat. 36 (2000), 153–165.Google Scholar
Assani, I.. Wiener Wintner Ergodic Theorems. World Science, River Edge, NJ, 2003.Google Scholar
Assani, I.. Pointwise double recurrence and nilsequences. Preprint, 2015, arXiv:1504.05732.Google Scholar
Assani, I., Duncan, D. and Moore, R.. Pointwise characteristic factors for Wiener–Wintner double recurrence theorem. Ergod. Th. & Dynam. Sys. (2015), available on CJO 2015; doi:10.1017/etds.2014.99.Google Scholar
Assani, I. and Moore, R.. Extension of Wiener–Wintner double recurrence theorem to polynomials. Available on http://www.unc.edu/math/Faculty/assani/WWDR_poly_final_abSept19.pdf, submitted, 2014.Google Scholar
Assani, I. and Moore, R.. A good universal weight for multiple recurrence averages with commuting transformations in norm. Preprint, 2015, arXiv:1506.05370.CrossRefGoogle Scholar
Assani, I. and Presser, K.. Pointwise characteristic factors for multiple term return times theorem. Preprint, 2003.Google Scholar
Assani, I. and Presser, K.. Pointwise characteristic factors for the multiterm return times theorem. Ergod. Th. & Dynam. Sys. 32 (2012), 341–360.Google Scholar
Assani, I. and Presser, K.. Survey of the return times theorem. Ergodic Theory and Dynamical Systems: Proceedings of the Ergodic Theory Workshops at University of North Carolina at Chapel Hill, 2011–2012 (De Gruyter Proceedings in Mathematics) . De Gruyter, Berlin, 2014, pp. 19–58.Google Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160 (2005), 261–303, with appendix by I. Ruzsa.CrossRefGoogle Scholar
Bourgain, J.. Return time sequences of dynamical systems. Preprint, 1988.Google Scholar
Bourgain, J.. Double recurrence and almost sure convergence. J. Reine Angew. Math. 404 (1990), 140–161.Google Scholar
Bourgain, J., Furstenberg, H., Katznelson, Y. and Ornstein, D.. Appendix on return-time sequences. Publ. Math. Inst. Hautes Études Sci. 69 (1989), 42–45.Google Scholar
Brunel, A.. Sur quelques problèmes de la thèorie ergodique ponctuelle. PhD Thesis, 1966.Google Scholar
Brunel, A. and Keane, M.. Ergodic theorems for operator sequences. Z. Wahrscheinlichkeitstheorie Verw. Geb. 12 (1969), 231–240.CrossRefGoogle Scholar
Eisner, T.. Linear sequences on weighted ergodic theorems. Abstr. Appl. Anal. (2013), Art ID. 815726.Google Scholar
Eisner, T. and Zorin-Kranich, P.. Uniformity in the Wiener–Wintner theorem for nilsequences. Discrete Contin. Dyn. Syst. 33(8) (2013), 3497–3516.Google Scholar
Gowers, W. T.. A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11 (2001), 465–588.Google Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161 (2005), 387–488.Google Scholar
Host, B. and Kra, B.. Uniformity seminorms on ℓ ∞ and applications. J. Anal. Math. 108 (2009), 219–276.Google Scholar
Krengel, U.. Ergodic Theorems (De Gruyter Studies in Mathematics, 6) . Walter de Gruyter, Berlin, 1985.Google Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. John Wiley and Sons, New York, 1974.Google Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequence of translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25 (2005), 201–213.CrossRefGoogle Scholar
Rudolph, D.. Fully generic sequences and a multiple-term return-times theorem. Invent. Math. 131(1) (1998), 199–228.Google Scholar
Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20(1) (2006), 53–97.Google Scholar
Zorin-Kranich, P.. Cube spaces and the multiple term return times theorem. Ergod. Th. & Dynam Sys. 34(5) (2014), 1747–1760.CrossRefGoogle Scholar
Zorin-Kranich, P.. A double return times theorem. Preprint, 2015, arXiv:1506.05748.Google Scholar
Zorin-Kranich, P.. A nilsequence Wiener–Wintner theorem for bilinear ergodic averages. Preprint, 2015,arXiv:1504.04647.Google Scholar