Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T10:44:36.288Z Has data issue: false hasContentIssue false
  • English
  • Français

A global two-dimensional version of Smale’s cancellation theorem via spectral sequences

Published online by Cambridge University Press:  19 March 2015

M. A. BERTOLIM ,
D. V. S. LIMA ,
M. P. MELLO ,
K. A. DE REZENDE  and
M. R. DA SILVEIRA
M. A. BERTOLIM
Affiliation:
Universitat Salzburg, Kapitelgasse 4–6, 5020, Salzburg, Austria email [email protected]
D. V. S. LIMA
Affiliation:
IMECC, Universidade Estadual de Campinas, Campinas, SP, CEP 13083-859, Brazil email [email protected], [email protected], [email protected]
M. P. MELLO
Affiliation:
IMECC, Universidade Estadual de Campinas, Campinas, SP, CEP 13083-859, Brazil email [email protected], [email protected], [email protected]
K. A. DE REZENDE
Affiliation:
IMECC, Universidade Estadual de Campinas, Campinas, SP, CEP 13083-859, Brazil email [email protected], [email protected], [email protected]
M. R. DA SILVEIRA
Affiliation:
CMCC, Universidade Federal do ABC, Santo André, SP, CEP 09210-580, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, Conley’s connection matrix theory and a spectral sequence analysis of a filtered Morse chain complex 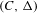$(C,{\rm\Delta})$ are used to study global continuation results for flows on surfaces. The briefly described unfoldings of Lyapunov graphs have been proved to be a well-suited combinatorial tool to keep track of continuations. The novelty herein is a global dynamical cancellation theorem inferred from the differentials of the spectral sequence 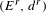$(E^{r},d^{r})$. The local version of this theorem relates differentials 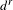$d^{r}$ of the $r$th page 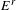$E^{r}$ to Smale’s theorem on cancellation of critical points.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 6 , September 2016 , pp. 1795 - 1838
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertolim, M. A., Lima, D. V. S., Mello, M. P., de Rezende, K. A. and da Silveira, M. R.. An algorithmic approach to algebraic and dynamical cancellations associated to a spectral sequence. Preprint, 2014, available at: arXiv:1408.6286 [math.DS].Google Scholar
Bertolim, M. A., Mello, M. P. and de Rezende, K. A.. Lyapunov graph continuation. Ergod. Th. & Dynam. Sys. 23(1) (2003), 1–58.Google Scholar
Bertolim, M. A., Mello, M. P. and de Rezende, K. A.. Dynamical and topological aspects of Lyapunov graphs. Qual. Theory Dyn. Syst. 4(2) (2004), 181–203.Google Scholar
Bertolim, M. A., Mello, M. P. and de Rezende, K. A.. Poincaré–Hopf and Morse inequalities for Lyapunov graphs. Ergod. Th. & Dynam. Sys. 25(1) (2005), 1–39.Google Scholar
Bertolim, M. A., de Rezende, K. A. and Manzoli Neto, O.. Isolating blocks for periodic orbits. J. Dyn. Control Syst. 13(1) (2007), 121–134.Google Scholar
Bertolim, M. A., de Rezende, K. A., Manzoli Neto, O. and Vago, G. M.. Isolating blocks for Morse flows. Geom. Dedicata 121 (2006), 19–41.Google Scholar
Bertolim, M. A., de Rezende, K. A., Manzoli Neto, O. and Vago, G. M.. On the variations of the Betti numbers of regular levels of Morse flows. Topology Appl. 158(6) (2011), 761–774.Google Scholar
Bertolim, M. A., de Rezende, K. A. and Vago, G. M.. Minimal Morse flows on compact manifolds. Topology Appl. 153(18) (2006), 3450–3466.Google Scholar
Biasotti, S., Giorgi, D., Spagnuolo, M. and Falcidieno, B.. Reeb graphs for shape analysis and applications. Theoret. Comput. Sci. 392 (2008), 5–22.Google Scholar
Bruce, J. W. and Giblin, P. J.. Curves and Singularities: a Geometrical Introduction to Singularity Theory, 2nd edn. Cambridge University Press, New York, 1992.Google Scholar
Conley, C.. Isolated Invariant Sets and the Morse Index (CBMS Regional Conference Series in Mathematics, 38) . American Mathematical Society, Providence, RI, 1978.Google Scholar
Conley, C. and Easton, R.. Isolated invariant sets and isolating blocks. Trans. Amer. Math. Soc. 158(1) (1971), 35–61.Google Scholar
Cornea, O., de Rezende, K. A. and da Silveira, M. R.. Spectral sequences in Conley’s theory. Ergod. Th. & Dynam. Sys. 30(4) (2010), 1009–1054.Google Scholar
Cruz, R. N., Mello, M. P. and de Rezende, K. A.. Realizability of the Morse polytope. Qual. Theory Dyn. Syst. 6(1) (2005), 59–86.CrossRefGoogle Scholar
Cruz, R. N. and de Rezende, K. A.. Cycle rank of Lyapunov graphs and the genera of manifolds. Proc. Amer. Math. Soc. 126(12) (1998), 3715–3720.Google Scholar
Cruz, R. N. and de Rezende, K. A.. Gradient-like flows on high-dimensional manifolds. Ergod. Th. & Dynam. Sys. 19(2) (1999), 339–362.Google Scholar
Davis, J. F. and Kirk, P.. Lecture Notes in Algebraic Topology (Graduate Studies in Mathematics, 35) . American Mathematical Society, Providence, RI, 2001.CrossRefGoogle Scholar
Edelsbrunner, H. and Harer, J.. Computational Topology. An Introduction. American Mathematical Society, Providence, RI, 2010.Google Scholar
Franks, J.. Homology and Dynamical Systems (CBMS Regional Conference Series in Mathematics, 49) . American Mathematical Society, Providence, RI, 1982.Google Scholar
Franks, J.. Nonsingular Smale flows on S 3 . Topology 24(3) (1985), 265–282.Google Scholar
Franzosa, R.. The connection matrix theory for Morse decompositions. Trans. Amer. Math. Soc. 311 (1989), 561–592.Google Scholar
Franzosa, R. D. and de Rezende, K. A.. Lyapunov graphs and flows on surfaces. Trans. Amer. Math. Soc. 340(2) (1993), 767–784.Google Scholar
Franzosa, R. D., de Rezende, K. A. and da Silveira, M. R.. Continuation and bifurcation associated to the dynamical spectral sequence. Ergod. Th. & Dynam. Sys. 34(6) (2014), 1849–1887.Google Scholar
Herlem, G., Ducellier, G., Adragna, P., Durupt, A. and Remy, S.. A reverse engineering method for DMU maturity management: use of a functional Reeb graph. IFIP Adv. Inf. Commun. Technol. 409 (2013), 422–431.Google Scholar
Khoury, R., Vandeborre, J. and Daoudi, M.. 3D mesh Reeb graph computation using commute-time and difusion distances. Proc. SPIE 8290 (2012), 8290H.Google Scholar
McCord, C.. The connection map for attractor–repeller pairs. Trans. Amer. Math. Soc. 307 (1988), 195–203.CrossRefGoogle Scholar
Mello, M. P., de Rezende, K. A. and da Silveira, M. R.. Conley’s spectral sequences via the sweeping algorithm. Topology Appl. 157(13) (2010), 2111–2130.Google Scholar
Milnor, J.. Lectures on the h-Cobordism Theorem. Princeton University Press, Princeton, NJ, 1965.CrossRefGoogle Scholar
Pepe, A., Brandolini, L., Piastra, M., Koikkalainen, J., Hietala, J. and Tohka, J.. Simplified Reeb graph as effective shape descriptor for the striatum. Mesh Processing in Medical Image Analysis 2012 (Lecture Notes in Computer Science, 7599) . Springer, Berlin, 2012, pp. 134–146.Google Scholar
Reeb, G.. Sur les points singuliers d’une forme de Pfaff complétement intégrable ou d’une fonction numérique. C. R. Acad. Sci. Paris 222 (1946), 847–849.Google Scholar
Reineck, J. F.. Continuation to the minimal number of critical points in gradient flows. Duke Math. J. 68 (1992), 185–194.Google Scholar
Salamon, D. A.. The Morse theory, the Conley index and the Floer homology. Bull. Lond. Math. Soc. 22 (1990), 113–240.CrossRefGoogle Scholar
Spanier, E.. Algebraic Topology. McGraw-Hill, New York, 1966.Google Scholar
Weber, J.. The Morse–Witten complex via dynamical systems. Expo. Math. 24 (2006), 127–159.Google Scholar
Zomorodian, A. J.. Topology for Computing. Cambridge University Press, New York, 2005.Google Scholar