Published online by Cambridge University Press: 19 September 2008
We improve and extend a result due to M. Kanai about rigidity of geodesic flows on closed Riemannian manifolds of negative curvature whose stable or unstable horospheric foliation is smooth. More precisely, the main results proved here are: (1) Let M be a closed C∞ Riemannian manifold of negative sectional curvature. Assume the stable or unstable foliation of the geodesic flow φt: V → V on the unit tangent bundle V of M is C∞. Assume, moreover, that either (a) the sectional curvature of M satisfies −4 < K ≤ −1 or (b) the dimension of M is odd. Then the geodesic flow of M is C∞-isomorphic (i.e., conjugate under a C∞ diffeomorphism between the unit tangent bundles) to the geodesic flow on a closed Riemannian manifold of constant negative curvature. (2) For M as above, assume instead of (a) or (b) that dim M ≡ 2(mod 4). Then either the above conclusion holds or φ1, is C∞-isomorphic to the flow 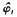 , on the quotient Γ\
, on the quotient Γ\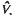 , where Γ is a subgroup of a real Lie group
, where Γ is a subgroup of a real Lie group 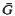 ⊂ Diffeo (
⊂ Diffeo (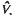 ) with Lie algebra
) with Lie algebra 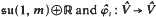 is the geodesic flow on the unit tangent bundle of the complex hyperbolic space ℂHm, m = ½ dim M.
is the geodesic flow on the unit tangent bundle of the complex hyperbolic space ℂHm, m = ½ dim M.