No CrossRef data available.
Published online by Cambridge University Press: 25 October 2021
Given a dynamical simplex K on a Cantor space X, we consider the set
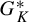 $G_K^*$
of all homeomorphisms of X which preserve all elements of K and have no non-trivial clopen invariant subset. Generalizing a theorem of Yingst, we prove that for a generic element g of
$G_K^*$
of all homeomorphisms of X which preserve all elements of K and have no non-trivial clopen invariant subset. Generalizing a theorem of Yingst, we prove that for a generic element g of
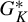 $G_K^*$
the set of invariant measures of g is equal to K. We also investigate when there exists a generic conjugacy class in
$G_K^*$
the set of invariant measures of g is equal to K. We also investigate when there exists a generic conjugacy class in
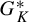 $G_K^*$
and prove that this happens exactly when K has only one element, which is the unique invariant measure associated to some odometer; and that in that case the conjugacy class of this odometer is generic in
$G_K^*$
and prove that this happens exactly when K has only one element, which is the unique invariant measure associated to some odometer; and that in that case the conjugacy class of this odometer is generic in
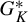 $G_K^*$
.
$G_K^*$
.