Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-13T12:01:42.840Z Has data issue: false hasContentIssue false
  • English
  • Français

The generalized recurrent set and strong chain recurrence

Published online by Cambridge University Press:  04 July 2016

JIM WISEMAN
JIM WISEMAN*
Affiliation:
Agnes Scott College, Mathematics, Decatur, Georgia 30030, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fathi and Pageault have recently shown a connection between Auslander’s generalized recurrent set 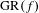$\text{GR}(f)$ and Easton’s strong chain recurrent set. We study 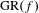$\text{GR}(f)$ by examining that connection in more detail, as well as connections with other notions of recurrence. We give equivalent definitions that do not refer to a metric. In particular, we show that 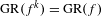$\text{GR}(f^{k})=\text{GR}(f)$ for any 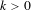$k>0$, and give a characterization of maps for which the generalized recurrent set is different from the ordinary chain recurrent set.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 2 , April 2018 , pp. 788 - 800
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbondandolo, A., Bernardi, O. and Cardin, F.. Chain recurrence, chain transitivity, Lyapunov functions and rigidity of Lagrangian submanifolds of optical hypersurfaces. Preprint, 2015.CrossRefGoogle Scholar
Akin, E.. The General Topology of Dynamical Systems (Graduate Studies in Mathematics, 1) . American Mathematical Society, Providence, RI, 1993.Google Scholar
Akin, E. and Auslander, J.. Generalized recurrence, compactifications, and the Lyapunov topology. Studia Math. 201(1) (2010), 49–63.Google Scholar
Akin, E., Hurley, M. and Kennedy, J. A.. Dynamics of topologically generic homeomorphisms. Mem. Amer. Math. Soc. 164(783) (2003), viii+130.Google Scholar
Auslander, J.. Generalized recurrence in dynamical systems. Contrib. Differ. Equ. 3 (1964), 65–74.Google Scholar
Auslander, J.. Non-compact dynamical systems. Recent Advances in Topological Dynamics (Proc. Conf., Yale University, New Haven, CT, 1972; in honor of Gustav Arnold Hedlund) (Lecture Notes in Mathematics, 318) . Springer, Berlin, 1973, pp. 6–11.Google Scholar
Birkhoff, G. D.. Dynamical Systems (American Mathematical Society Colloquium Publications, IX) . American Mathematical Society, Providence, RI, 1966.Google Scholar
Coven, E. M. and Nitecki, Z.. Nonwandering sets of the powers of maps of the interval. Ergod. Th. & Dynam. Sys. 1(1) (1981), 9–31.Google Scholar
Easton, R.. Chain transitivity and the domain of influence of an invariant set. The Structure of Attractors in Dynamical Systems (Proc. Conf., North Dakota State University, Fargo, ND, 1977) (Lecture Notes in Mathematics, 668) . Springer, Berlin, 1978, pp. 95–102.Google Scholar
Fathi, A. and Pageault, P.. Aubry–Mather theory for homeomorphisms. Ergod. Th. & Dynam. Sys. 35(4) (2015), 1187–1207.Google Scholar
Franks, J.. A variation on the Poincaré–Birkhoff theorem. Hamiltonian Dynamical Systems (Boulder, CO, 1987) (Contemporary Mathematics, 81) . American Mathematical Society, Providence, RI, 1988, pp. 111–117.Google Scholar
Garay, B. M.. Auslander recurrence and metrization via Liapunov functions. Funkcial. Ekvac. 28(3) (1985), 299–308.Google Scholar
Kelley, J. L.. General Topology. Van Nostrand, New York, 1955.Google Scholar
Kotus, J. and Klok, F.. A sufficient condition for 𝛺-stability of vector fields on open manifolds. Compositio Math. 65(2) (1988), 171–176.Google Scholar
Nitecki, Z.. Explosions in completely unstable flows. I. Preventing explosions. Trans. Amer. Math. Soc. 245 (1978), 43–61.Google Scholar
Nitecki, Z.. Recurrent structure of completely unstable flows on surfaces of finite Euler characteristic. Amer. J. Math. 103(1) (1981), 143–180.Google Scholar
Paradís, J., Viader, P. and Bibiloni, L.. The derivative of Minkowski’s ? (x) function. J. Math. Anal. Appl. 253(1) (2001), 107–125.Google Scholar
Peixoto, M. L. A.. Characterizing 𝛺-stability for flows in the plane. Proc. Amer. Math. Soc. 104(3) (1988), 981–984.Google Scholar
Peixoto, M. L. A.. The closing lemma for generalized recurrence in the plane. Trans. Amer. Math. Soc. 308(1) (1988), 143–158.Google Scholar
Pesin, Y. B.. Dimension theory in dynamical systems. Contemporary Views and Applications (Chicago Lectures in Mathematics) . University of Chicago Press, Chicago, 1997.Google Scholar
Richeson, D. and Wiseman, J.. Chain recurrence rates and topological entropy. Topology Appl. 156(2) (2008), 251–261.CrossRefGoogle Scholar
Sawada, K.. On the iterations of diffeomorphisms without C 0-𝛺-explosions: an example. Proc. Amer. Math. Soc. 79(1) (1980), 110–112.Google Scholar
Sierpiński, W.. General Topology (Mathematical Expositions, 7) . Transl. C. Cecilia Krieger. University of Toronto Press, Toronto, 1952.Google Scholar
Souza, J. A. and Tozatti, H. V. M.. Prolongational limit sets of control systems. J. Differential Equations 254(5) (2013), 2183–2195.Google Scholar
Souza, J. A. and Tozatti, H. V. M.. Some aspects of stability for semigroup actions and control systems. J. Dynam. Differential Equations 26(3) (2014), 631–654.Google Scholar
Yokoi, K.. On strong chain recurrence for maps. Ann. Polon. Math. 114 (2015), 165–177.Google Scholar
Zheng, Z.-H.. Chain transitivity and Lipschitz ergodicity. Nonlinear Anal. 34(5) (1998), 733–744.Google Scholar