Published online by Cambridge University Press: 14 February 2017
We study the interplay between the dynamics of area-preserving surface homeomorphisms homotopic to the identity and the topology of the surface. We define fully essential dynamics and generalize the results previously obtained on strictly toral dynamics to surfaces of higher genus. Non-fully essential dynamics are, in a way, reducible to surfaces of lower genus, while in the fully essential case the dynamics is decomposed into a disjoint union of periodic bounded disks and a complementary invariant externally transitive continuum  $C$. When the Misiurewicz–Ziemian rotation set has non-empty interior the dynamics is fully essential, and the set
$C$. When the Misiurewicz–Ziemian rotation set has non-empty interior the dynamics is fully essential, and the set 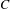 $C$ is (externally) sensitive on initial conditions and realizes all of the rotational dynamics. As a fundamental tool we introduce the notion of homotopically bounded sets and we prove a general boundedness result for invariant open sets when the fixed point set is inessential.
$C$ is (externally) sensitive on initial conditions and realizes all of the rotational dynamics. As a fundamental tool we introduce the notion of homotopically bounded sets and we prove a general boundedness result for invariant open sets when the fixed point set is inessential.