Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T09:00:29.787Z Has data issue: false hasContentIssue false
  • English
  • Français

From the divergence between two measures to the shortest path between two observables

Published online by Cambridge University Press:  28 November 2017

MIGUEL ABADI  and
RODRIGO LAMBERT
MIGUEL ABADI
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão, 1010, CEP 05508-090, São Paulo-SP, Brazil email [email protected]
RODRIGO LAMBERT
Affiliation:
Faculdade de Matemática, Universidade Federal de Uberlândia, Av. João Naves de Avila, 2121, CEP 38408-100, Uberlândia-MG, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider two independent and stationary measures over 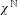$\unicode[STIX]{x1D712}^{\mathbb{N}}$, where $\unicode[STIX]{x1D712}$ is a finite or countable alphabet. For each pair of $n$-strings in the product space we define 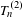$T_{n}^{(2)}$ as the length of the shortest path connecting one of them to the other. Here the paths are generated by the underlying dynamic of the measures. If they are ergodic and have positive entropy we prove that, for almost every pair of realizations 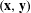$(\mathbf{x},\mathbf{y})$, 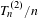$T_{n}^{(2)}/n$ is concentrated in one, as $n$ diverges. Under mild extra conditions we prove a large-deviation principle. We also show that the fluctuations of 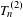$T_{n}^{(2)}$ converge (only) in distribution to a non-degenerate distribution. These results are all linked to a quantity that computes the similarity between those two measures. This is the so-called divergence between two measures, which is also introduced. Several examples are provided.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 7 , July 2019 , pp. 1729 - 1744
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abadi, M. and Cardeno, L.. Renyi entropies and large deviations for the first-match function. IEEE Trans. Inform. Theory 61(4) (2015), 1629–1639.Google Scholar
Abadi, M., Gallo, S. and Rada, E.. The shortest possible return time of $\unicode[STIX]{x1D6FD}$ -mixing processes. IEEE Trans. Inf. Theory to appear. Available online at http://ieeexplore.ieee.org/document/8052545/.Google Scholar
Abadi, M. and Lambert, R.. The distribution of the short-return function. Nolinearity 26(5) (2013), 1143–1162.Google Scholar
Abadi, M. and Vaienti, S.. Large deviations for short recurrence. Discrete Contin. Dyn. Syst. 21 (2008), 729–747.Google Scholar
Afraimovich, V., Chazottes, J.-R. and Saussol, B.. Point-wise dimensions for Poincaré recurrence associated with maps and special flows. Discrete Contin. Dyn. Syst. 9(2) (2003), 263–280.Google Scholar
Bauckhage, C., Kersting, K. and Rastegarpanah, B.. The Weibull as a model of shortest path distributions in random networks, avaliable online at http://snap.stanford.edu/mlg2013/submissions/mlg2013_submission_5.pdf.Google Scholar
Blondel, V., Guillaume, J., Hendrickx, J. and Jungers, R.. Distance distribution in random graphs and application to network exploration. Phys. Rev. E 76 (2007), 066101.Google Scholar
Bowen, R.. Periodic points and measures for Axiom A diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Cover, T. and Thomas, J.. Elements of Information Theory, 2nd edn. Wiley, New York, 1991.Google Scholar
Haydn, N. and Vaienti, S.. The Renyi entropy function and the large deviation of short return times. Ergod. Th. & Dynam. Sys. 30(1) (2010), 159–179.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Math. and its Applications, 54) . Cambridge University Press, Cambridge, 1995.Google Scholar
Katzav, E., Nitzan, M., ben-Avraham, D., Krapivsky, P., Kühn, R., Ross, N. and Biham, O.. Analytical results for the distribution of shortest path lengths in random networks. Europhys. Lett. 111(2) (2015), 26006.Google Scholar
Kontoyiannis, I.. Asymptotic recurrence and waiting times for stationary processes. J. Theoret. Probab. 11(3) (1998), 795–811.Google Scholar
Marton, K. and Shields, P.. Almost-sure waiting time results for weak and very weak Bernoulli processes. Ergod. Th. & Dynam. Sys. 15 (1995), 951–960.Google Scholar
Nobel, A. and Wyner, A. D.. A recurrence theorem for dependent processes with applications to data compression. IEEE Trans. Inform. Theory 38 (1992), 1561–1564.Google Scholar
Rocha, A.. Substitution operators. PhD Thesis, Universidade Federal de Pernambuco, 2009. Avaliable online at http://toomandre.com/alunos/doutorado/andrea/tese-andrea.pdf.Google Scholar
Saussol, B., Troubetzkoy, S. and Vaienti, S.. Recurrence, dimensions and Lyapunov exponents. J. Stat. Phys. 106 (2002), 623–634.Google Scholar
Shields, P.. Waiting times: positive and negative results on the Wyner–Ziv problem. J. Theoret. Probab. 6 (1993), 499–519.Google Scholar
Sigmund, K.. On dynamical systems with the specification property. Trans. Amer. Math. Soc. 190 (1974), 285–299.Google Scholar
Sumi, N., Varandas, P. and Yamamoto, K.. Partial hyperbolicity and specification. Proc. Amer. Math. Soc. 144 (2016), 1161–1170.Google Scholar
Ukkonen, A.. Indirect estimation of shortest path distributions with small-world experiments. Advances in Intelligent Data Analysis XIII: Proceedings of the 13th International Symposium, IDA 2014 Leuven, Belgium, October 30–November 1, 2014 (Lecture Notes in Computer Science, 8819) . Springer, Cham, 2014, pp. 333–344.Google Scholar
Varandas, P.. Non-uniform specification and large deviations for weak Gibbs measures. J. Stat. Phys. 146(2) (2012), 330–358.Google Scholar
Vazquez, A.. Polynomial growth in branching processes with diverging reproduction number. Phys. Rev. Lett. 96 (2006),038702.Google Scholar
Wyner, A.. More on recurrence and waiting times. Ann. Appl. Probab. 9(3) (1999), 780–796.Google Scholar
Wyner, A. and Ziv, J.. Some asymptotic properties of the entropy of a stationary ergodic data source with applications to data compression. IEEE Trans. Inform. Theory 35(6) (1989), 1250–1258.Google Scholar
Yamamoto, K.. On the weaker forms of the specification property and their applications. Proc. Amer. Math. Soc. 137(11) (2009), 3807–3814.Google Scholar