Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T17:56:27.769Z Has data issue: false hasContentIssue false
  • English
  • Français

Four-cycle free graphs, height functions, the pivot property and entropy minimality

Published online by Cambridge University Press:  08 March 2016

NISHANT CHANDGOTIA
NISHANT CHANDGOTIA*
Affiliation:
Department of Mathematics, University of British Columbia, Canada email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fix 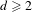$d\geq 2$. Given a finite undirected graph 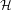${\mathcal{H}}$ without self-loops and multiple edges, consider the corresponding ‘vertex’ shift, 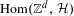$\text{Hom}(\mathbb{Z}^{d},{\mathcal{H}})$, denoted by 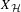$X_{{\mathcal{H}}}$. In this paper, we focus on 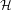${\mathcal{H}}$ which is ‘four-cycle free’. There are two main results of this paper. Firstly, that 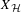$X_{{\mathcal{H}}}$ has the pivot property, meaning that, for all distinct configurations 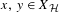$x,y\in X_{{\mathcal{H}}}$, which differ only at a finite number of sites, there is a sequence of configurations 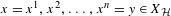$x=x^{1},x^{2},\ldots ,x^{n}=y\in X_{{\mathcal{H}}}$ for which the successive configurations 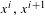$x^{i},x^{i+1}$ differ exactly at a single site. Secondly, if 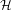${\mathcal{H}}$ is connected ,then 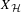$X_{{\mathcal{H}}}$ is entropy minimal, meaning that every shift space strictly contained in 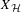$X_{{\mathcal{H}}}$ has strictly smaller entropy. The proofs of these seemingly disparate statements are related by the use of the ‘lifts’ of the configurations in 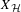$X_{{\mathcal{H}}}$ to the universal cover of 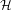${\mathcal{H}}$ and the introduction of ‘height functions’ in this context.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1102 - 1132
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angluin, D.. Local and global properties in networks of processors (extended abstract). Proc. 12th Ann. ACM Symp. on Theory of Computing (Los Angeles, CA, USA, 28–30 April 1980). ACM, New York, 1980, pp. 82–93.Google Scholar
Boyle, M., Pavlov, R. and Schraudner, M.. Multidimensional sofic shifts without separation and their factors. Trans. Amer. Math. Soc. 362(9) (2010), 4617–4653.CrossRefGoogle Scholar
Briceño, R.. The topological strong spatial mixing property and new conditions for pressure approximation. Preprint, 2014, arXiv:org/abs/1411.2289.Google Scholar
Brightwell, G. R. and Winkler, P.. Gibbs measures and dismantlable graphs. J. Combin. Theory Ser. B 78(1) (2000), 141–166.Google Scholar
Capobianco, S.. Multidimensional cellular automata and generalization of Fekete’s lemma. Discrete Math. Theor. Comput. Sci. 10(3) (2008), 95–104.Google Scholar
Chandgotia, N.. Generalisation of the Hammersley–Clifford theorem on bipartite graphs. Preprint, 2014,arXiv:org/abs/1406.1849.Google Scholar
Chandgotia, N. and Meyerovitch, T.. Markov random fields, Markov cocycles and the 3-colored chessboard. Preprint, 2013, arXiv:org/abs/1305.0808.Google Scholar
Coven, E. M. and Smítal, J.. Entropy-minimality. Acta Math. Univ. Comenian. (N.S.) 62(1) (1993), 117–121.Google Scholar
Folland, G. B.. Real Analysis: Modern Techniques and their Applications (Pure and Applied Mathematics (New York)) , 2nd edn. Wiley-Interscience, New York, 1999.Google Scholar
Friedland, S.. On the entropy of Z d subshifts of finite type. Linear Algebra Appl. 252 (1997), 199–220.Google Scholar
Georgii, H.-O.. Gibbs Measures and Phase Transitions (de Gruyter Studies in Mathematics, 9) . Walter de Gruyter & Co., Berlin, 1988.Google Scholar
Hammersley, J. M. and Welsh, D. J. A.. First-passage percolation, subadditive processes, stochastic networks, and generalized renewal theory. Proc. Int. Res. Semin. (Statistics Laboratory, University of California). Springer, New York, 1965, pp. 61–110.Google Scholar
Keller, G.. Equilibrium States in Ergodic Theory (London Mathematical Society Student Texts, 42) . Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Lanford, O. E. III and Ruelle, D.. Observables at infinity and states with short range correlations in statistical mechanics. Comm. Math. Phys. 13 (1969), 194–215.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995, reprinted 1999.Google Scholar
Louidor, E. and Marcus, B. H.. Improved lower bounds on capacities of symmetric 2D constraints using Rayleigh quotients. IEEE Trans. Inform. Theory 56(4) (2010), 1624–1639.Google Scholar
Massey, W. S.. Algebraic Topology: an Introduction (Graduate Texts in Mathematics, 56) . Springer, New York, 1977, reprint of the 1967 edition.Google Scholar
Meester, R. and Steif, J. E.. Higher-dimensional subshifts of finite type, factor maps and measures of maximal entropy. Pacific J. Math. 200(2) (2001), 497–510.Google Scholar
Munkres, J. R.. Topology: A First Course. Prentice-Hall, Englewood Cliffs, NJ, 1975.Google Scholar
Nakano, F., Ono, H. and Sadahiro, T.. Local move connectedness of domino tilings with diagonal impurities. Discrete Math. 310(13–14) (2010), 1918–1931.Google Scholar
Nowakowski, R. and Winkler, P.. Vertex-to-vertex pursuit in a graph. Discrete Math. 43(2–3) (1983), 235–239.CrossRefGoogle Scholar
Ordentlich, E. and Roth, R. M.. When data must satisfy constraints upon writing. Proc. IEEE Int. Symp. on Information Theory (Honolulu, Hawaii, June 2014). IEEE, Piscataway, NJ, 2014, pp. 2257–2261.Google Scholar
Pavlov, R.. Approximating the hard square entropy constant with probabilistic methods. Ann. Probab. 40(6) (2012), 2362–2399.CrossRefGoogle Scholar
Peled, R.. High-dimensional Lipschitz functions are typically flat. Ann. Probab. to appear. Preprint, 2010,arXiv:org/abs/1005.4636.Google Scholar
Petersen, K. and Schmidt, K.. Symmetric Gibbs measures. Trans. Amer. Math. Soc. 349(7) (1997), 2775–2811.CrossRefGoogle Scholar
Quas, A. N. and Trow, P. B.. Subshifts of multi-dimensional shifts of finite type. Ergod. Th. & Dynam. Sys. 20(3) (2000), 859–874.CrossRefGoogle Scholar
Robinson, R. M.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.Google Scholar
Ruelle, D.. Thermodynamic Formalism: The Mathematical Structures of Equilibrium Statistical Mechanics, 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Schmidt, K.. The cohomology of higher-dimensional shifts of finite type. Pacific J. Math. 170(1) (1995), 237–269.Google Scholar
Schmidt, K.. Invariant cocycles, random tilings and the super-K and strong Markov properties. Trans. Amer. Math. Soc. 349(7) (1997), 2813–2825.Google Scholar
Schmidt, K.. Tilings, fundamental cocycles and fundamental groups of symbolic ℤ d -actions. Ergod. Th. & Dynam. Sys. 18(6) (1998), 1473–1525.Google Scholar
Schraudner, M.. Projectional entropy and the electrical wire shift. Discrete Contin. Dyn. Syst. 26(1) (2010), 333–346.Google Scholar
Schraudner, M. and Lightwood, S.. Entropy minimality of Zd shifts of finite type and the family of wire shifts. Work in progress.Google Scholar
Sheffield, S.. Ribbon tilings and multidimensional height functions. Trans. Amer. Math. Soc. 354(12) (2002), 4789–4813 (electronic).Google Scholar
Stallings, J. R.. Topology of finite graphs. Invent. Math. 71(3) (1983), 551–565.Google Scholar
Thurston, W. P.. Conway’s tiling groups. Amer. Math. Monthly 97(8) (1990), 757–773.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar
Wrochna, M.. Homomorphism reconfiguration via homotopy. 32nd Int. Symp. on Theoretical Aspects of Computer Science (STACS, 2015) (Leibniz International Proceedings in Informatics, 30) . Eds. Mayr, E. W. and Portier, N.. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany, 2015, pp. 730–742.Google Scholar