Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T10:49:47.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixed points of nilpotent actions on 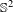$\mathbb{S}^{2}$

Published online by Cambridge University Press:  05 August 2014

JAVIER RIBÓN
JAVIER RIBÓN*
Affiliation:
Instituto de Matemática, UFF, Rua Mário Santos Braga S/N Valonguinho, Niterói, Rio de Janeiro, 24020-140, Brasil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that a nilpotent subgroup of orientation-preserving 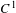$C^{1}$ diffeomorphisms of 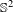$\mathbb{S}^{2}$ has a finite orbit of cardinality at most two. We also prove that a finitely generated nilpotent subgroup of orientation-preserving 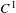$C^{1}$ diffeomorphisms of 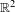$\mathbb{R}^{2}$ preserving a compact set has a global fixed point. These results generalize theorems of Franks et al for the abelian case. We show that a nilpotent subgroup of orientation-preserving 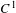$C^{1}$ diffeomorphisms of 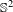$\mathbb{S}^{2}$ that has a finite orbit of odd cardinality also has a global fixed point. Moreover, we study the properties of the 2-points orbits of nilpotent fixed-point-free subgroups of orientation-preserving 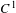$C^{1}$ diffeomorphisms of 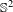$\mathbb{S}^{2}$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 1 , February 2016 , pp. 173 - 197
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baumslag, G.. Lecture Notes on Nilpotent Groups (Regional Conference Series in Mathematics, 2). American Mathematical Society, Providence, RI, 1971.Google Scholar
Birman, J. S., Lubotzky, A. and McCarthy, J.. Abelian and solvable subgroups of the mapping class groups. Duke Math. J. 50(4) (1983), 1107–1120.CrossRefGoogle Scholar
Bonatti, C.. Un point fixe commun pour des difféomorphismes commutants de S 2. Ann. of Math. (2) 129(1) (1989), 61–69.CrossRefGoogle Scholar
Bonatti, C.. Difféomorphismes commutants des surfaces et stabilité des fibrations en tores. Topology 29(1) (1990), 101–126.CrossRefGoogle Scholar
Brouwer, L. E. J.. Beweis des ebenen Translationssatzes. Math. Ann. 72 (1912), 37–54.CrossRefGoogle Scholar
Brown, M.. A short short proof of the Cartwright–Littlewood theorem. Proc. Amer. Math. Soc. 65(2) (1977), 372.Google Scholar
Cartwright, M. L. and Littlewood, J. E.. Some fixed point theorems. Ann. of Math. (2) 54 (1951), 1–37. With appendix by H. D. Ursell.CrossRefGoogle Scholar
Druck, S., Fang, F. and Firmo, S.. Fixed points of discrete nilpotent group actions on S 2. Ann. Inst. Fourier (Grenoble) 52(4) (2002), 1075–1091.CrossRefGoogle Scholar
Firmo, S., Ribón, J. and Velasco, J.. Fixed points for nilpotent actions on the plane and the Cartwright–Littlewood theorem. Preprint, 2013, arXiv:1306.0232 Math. Z. accepted for publication.CrossRefGoogle Scholar
Franks, J., Handel, M. and Parwani, K.. Fixed points of abelian actions. J. Mod. Dyn. 1(3) (2007), 443–464.CrossRefGoogle Scholar
Franks, J., Handel, M. and Parwani, K.. Fixed points of abelian actions on S 2. Ergod. Th. & Dynam. Sys. 27(5) (2007), 1557–1581.CrossRefGoogle Scholar
Gambaudo, J.-M.. Periodic orbits and fixed points of a C 1 orientation-preserving embedding of D 2. Math. Proc. Cambridge Philos. Soc. 108(2) (1990), 307–310.CrossRefGoogle Scholar
Ghys, É.. Sur les groupes engendrés par des difféomorphismes proches de l’identité. Bol. Soc. Brasil. Mat. (N.S.) 24(2) (1993), 137–178.CrossRefGoogle Scholar
Handel, M.. Commuting homeomorphisms of S 2. Topology 31(2) (1992), 293–303.CrossRefGoogle Scholar
Kerckhoff, S. P.. The Nielsen realization problem. Ann. of Math. (2) 117(2) (1983), 235–265.CrossRefGoogle Scholar
Kneser, H.. Die Deformationssätze der einfach zusammenhängenden Flächen. Math. Z. 25(1) (1926), 362–372.CrossRefGoogle Scholar
Le Calvez, P.. Pourquoi les points périodiques des homéomorphismes du plan tournent-ils autour de certains points fixes? Ann. Sci. Éc. Norm. Supér. (4) 41(1) (2008), 141–176.CrossRefGoogle Scholar
Lima, E. L.. Common singularities of commuting vector fields on 2-manifolds. Comment. Math. Helv. 39 (1964), 97–110.CrossRefGoogle Scholar
Navas, A.. Sur les rapprochements par conjugaison en dimension $1$ et classe $C^{1}$. Compos. Math. (2013),arXiv:1208.4815, to appear. Available on CJO2014 10.1112/S0010437X13007811.Google Scholar
Parkhe, K.. Smoothing nilpotent actions on 1-manifolds. Preprint, 2014, arXiv:1403.7781.Google Scholar
Plante, J. F.. Fixed points of Lie group actions on surfaces. Ergod. Th. & Dynam. Sys. 6(1) (1986), 149–161.CrossRefGoogle Scholar
Raghunathan, M. S.. Discrete Subgroups of Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, 68). Springer, New York, 1972.CrossRefGoogle Scholar
Serre, J.-P.. Trees (Springer Monographs in Mathematics). Springer, Berlin, 2003. Translated from the French original by John Stillwell. Corrected 2nd printing of the 1980 English translation.Google Scholar
Shurman, J.. Geometry of The Quintic. John Wiley & Sons, New York, 1997.Google Scholar