Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:16:23.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixed points of local actions of nilpotent Lie groups on surfaces

Published online by Cambridge University Press:  28 January 2016

MORRIS W. HIRSCH
MORRIS W. HIRSCH*
Affiliation:
Mathematics Department, University of Wisconsin, Madison, WI, USA University of California, Berkeley, CA, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 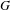$G$ be a connected nilpotent Lie group with a continuous local action on a real surface 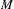$M$, which might be non-compact or have non-empty boundary $\unicode[STIX]{x2202}M$. The action need not be smooth. Let $\unicode[STIX]{x1D711}$ be the local flow on $M$ induced by the action of some one-parameter subgroup. Assume $K$ is a compact set of fixed points of $\unicode[STIX]{x1D711}$ and $U$ is a neighborhood of 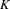$K$ containing no other fixed points.

Theorem.If the Dold fixed-point index of$\unicode[STIX]{x1D711}_{t}|U$is non-zero for sufficiently small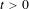$t>0$, then$\mathsf{Fix}(G)\cap K\neq \varnothing$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1238 - 1252
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belliart, M.. Actions sans points fixes sur les surfaces compactes. Math. Z. 225 (1997), 453–465.Google Scholar
Belliart, M. and Liousse, I.. Actions affines sur les surfaces (Publications IRMA, 38), Universite de Lille, 1996 exposé X.Google Scholar
Bohr, H. and Fenchel, W.. Ein Satz über stabile Bewgungen in der Ebene. Det Kongelige Danske Videnskabernes Selskab, Mathematisk-Fysiske Meddelelser 14(1), (1936). In: ‘Harald Bohr, Collected Mathematical Works, Vol. II,’ Danish Math. Soc., University of Copenhagen 1952.Google Scholar
Bonatti, C.. Champs de vecteurs analytiques commutants, en dimension 3 ou 4: existence de zéros communs. Bol. Soc. Brasil. Mat. (N.S.) 22 (1992), 215–247.Google Scholar
Ciesielski, K.. The Poincaré–Bendixson theorem: from Poincaré to the XXIst century. Cent. Eur. J. Math. 10(6) (2012), 2110–2128.Google Scholar
Dold, A.. Fixed point index and fixed point theorem for Euclidean neighborhood retracts. Topology 4 (1965), 1–8.Google Scholar
Dold, A.. Lectures on Algebraic Topology (Die Grundlehren der matematischen Wissenschaften Bd., 52) , 2nd edn. Springer, New York, 1972.Google Scholar
Epstein, D. B. A. and Thurston, W. P.. Transformation groups and natural bundles. Proc. Lond. Math. Soc. 38 (1979), 219–236.Google Scholar
Foland, N. E.. The Structure of the orbits and their limit sets in continuous flows. Pac. J. Math. 13 (1963), 563–570.Google Scholar
Hájek, O.. Structure of dynamical systems. Comment. Math. Univ. Carolin. 6 (1965), 53–72.Google Scholar
Hájek, O.. Dynamical Systems in The Plane. Academic Press, London, New York, 1968.Google Scholar
Hartman, P.. Ordinary Differential Equations. John Wiley & Sons, New York, 1964.Google Scholar
Hirsch, M. W.. Actions of Lie groups and Lie algebras on manifolds. A Celebration of the Mathematical Legacy of Raoul Bott (Centre de Recherches Mathématiques, U. de Montréal. Proceedings & Lecture Notes, 50) . Ed. Kotiuga, P. R.. American Mathematical Society, Providence, RI, 2010, pp. 69–78.Google Scholar
Hirsch, M. W.. Smooth actions of Lie groups and Lie algebras on manifolds. J. Fixed Point Theory Appl. 10 (2011), 219–232.Google Scholar
Hirsch, M. W.. Zero sets of Lie algebras of analytic vector fields on real and complex $2$ -manifolds. In preparation, 2014.Google Scholar
Hirsch, M. W. and Weinstein, A.. Fixed points of analytic actions of supersoluble Lie groups on compact surfaces. Ergod. Th. & Dynam. Sys. 21 (2001), 1783–1787.Google Scholar
Hopf, H.. Vektorfelder in Mannifaltigkeiten. Math. Ann. 95 (1925), 340–367.Google Scholar
Horne, J.. A locally compact connected group acting on the plane has a closed orbit. Illinois J. Math. 9 (1965), 644–650.CrossRefGoogle Scholar
Hounie, J.. Minimal sets of families of vector fields on compact surfaces. J. Differential Geom. 16 (1981), 739–744.Google Scholar
Lefschetz, S.. Intersections and transformations of complexes and manifolds. Trans. Amer. Math. Soc. 28 (1926), 1–49.Google Scholar
Lima, E.. Common singularities of commuting vector fields on 2-manifolds. Comment. Math. Helv. 39 (1964), 97–110.Google Scholar
Markley, N.. The Poincaré–Bendixson theorem for the Klein bottle. Trans. Amer. Math. Soc. 135 (1969), 159–165.Google Scholar
Markley, N.. On the number of recurrent orbit closures. Proc. Amer. Math. Soc. 25 (1970), 413–416.Google Scholar
Molino, P.. Review of Bonatti ‘Bol. Soc. Brasil. Mat. (N.S.) 22 (1992), 215–247’. Math. Reviews (1993), MR 1179486 (93h:57044).Google Scholar
Molino, P. and Turiel, F.-J.. Une observation sur les actions de R p sur les variétés compactes de caractéristique non nulle. Comment. Math. Helv. 61 (1986), 370–375.Google Scholar
Palais, R. S.. A Global Formulation of the Lie Theory of Transformation Groups (Memoirs American Mathematical Society, 22) . American Mathematical Society, Providence, RI, 1957.Google Scholar
Plante, J.. Foliations with measure preserving holonomy. Ann. of Math. (2) 102 (1975), 327–361.Google Scholar
Plante, J.. Fixed points of Lie group actions on surfaces. Ergod. Th. & Dynam. Sys. 6 (1986), 149–161.Google Scholar
Poincaré, H.. Sur les courbes définies par une équation différentielle. J. Math. Pures Appl. 1 (1885), 167–244.Google Scholar
Schwartz, A. J.. Generalization of a Poincaré–Bendixson theorem to closed two dimensional manifolds. Amer. J. Math. 85 (1963), 453–458.Google Scholar
Sacksteder, R.. Degeneracy of orbits of ℝ m acting on a manifold. Comm. Math. Helv. 41 (1966–67), 1–9.Google Scholar
Seibert, P. and Tulley, P.. On dynamical systems in the plane. Arch. Math. (Basel) 18 (1967), 290–292.Google Scholar
Turiel, F.-J.. An elementary proof of a Lima’s theorem for surfaces. Publ. Mat. 3 (1989), 555–557.Google Scholar
Turiel, F.-J.. Analytic actions on compact surfaces and fixed points. Manuscripta Math. 110 (2003), 195–201.Google Scholar
Varadarajan, V.. Lie Groups, Lie Algebras, and Their Representations. Springer, New York, 1976.Google Scholar
Whitney, H.. On regular families of curves. Bull. Amer. Math. Soc. 47 (1941), 145–147.Google Scholar