Published online by Cambridge University Press: 29 July 2016
Extensive amenability is a property of group actions which has recently been used as a tool to prove amenability of groups. We study this property and prove that it is preserved under a very general construction of semidirect products. As an application, we establish the amenability of all subgroups of the group  $\text{IET}$ of interval exchange transformations that have angular components of rational rank less than or equal to two. In addition, we obtain a reformulation of extensive amenability in terms of inverted orbits and use it to present a purely probabilistic proof that recurrent actions are extensively amenable. Finally, we study the triviality of the Poisson boundary for random walks on
$\text{IET}$ of interval exchange transformations that have angular components of rational rank less than or equal to two. In addition, we obtain a reformulation of extensive amenability in terms of inverted orbits and use it to present a purely probabilistic proof that recurrent actions are extensively amenable. Finally, we study the triviality of the Poisson boundary for random walks on 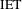 $\text{IET}$ and show that there are subgroups
$\text{IET}$ and show that there are subgroups 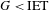 $G<\text{IET}$ admitting no finitely supported measure with trivial boundary.
$G<\text{IET}$ admitting no finitely supported measure with trivial boundary.