Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-25T10:36:58.122Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of the zero-temperature limit of equilibrium states on topologically transitive countable Markov shifts

Part of: Ergodic theory Markov processes Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  04 October 2022

ELMER BELTRÁN Open the ORCID record for ELMER BELTRÁN [Opens in a new window] ,
JORGE LITTIN Open the ORCID record for JORGE LITTIN [Opens in a new window] ,
CESAR MALDONADO Open the ORCID record for CESAR MALDONADO [Opens in a new window]  and
VICTOR VARGAS Open the ORCID record for VICTOR VARGAS [Opens in a new window]
ELMER BELTRÁN
Affiliation:
Departamento de Matemáticas, Universidad Católica del Norte, Avenida Angamos 0610, Antofagasta, Chile (e-mail: [email protected])
JORGE LITTIN*
Affiliation:
Departamento de Matemáticas, Universidad Católica del Norte, Avenida Angamos 0610, Antofagasta, Chile (e-mail: [email protected])
CESAR MALDONADO
Affiliation:
IPICYT, División de Control y Sistemas Dinámicos, Camino a la Presa San José 2055, Lomas 4a. sección, San Luis Potosí, México (e-mail: [email protected])
VICTOR VARGAS
Affiliation:
Center for Mathematics of the University of Porto, Rua do Campo Alegre 687, Porto, Portugal (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

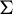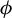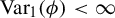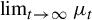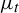Consider a topologically transitive countable Markov shift $\Sigma $ and a summable locally constant potential $\phi $ with finite Gurevich pressure and $\mathrm {Var}_1(\phi ) < \infty $. We prove the existence of the limit $\lim _{t \to \infty } \mu _t$ in the weak$^\star $ topology, where $\mu _t$ is the unique equilibrium state associated to the potential 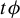$t\phi $. In addition, we present examples where the limit at zero temperature exists for potentials satisfying more general conditions.

Keywords

countable Markov shiftequilibrium statemaximizing measurerenewal shiftstationary Markov measuretopologically transitive

MSC classification

Primary: 37A30: Ergodic theorems, spectral theory, Markov operators 37A60: Dynamical systems in statistical mechanics 37D35: Thermodynamic formalism, variational principles, equilibrium states
Secondary: 60J05: Discrete-time Markov processes on general state spaces 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 10 , October 2023 , pp. 3231 - 3254
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baraviera, A., Leplaideur, R. and Lopes, A. O.. Ergodic optimization, zero temperature limits and the max-plus algebra. Paper from the 29th Brazilian Mathematics Colloquium – 29 Colóquio Brasileiro de Matemática, Rio de Janeiro, Brazil, July 22–August 2, 2013. Instituto Nacional de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, 2013.Google Scholar
Beltrán, E. R., Bissacot, R. and Endo, E. O.. Infinite DLR measures and volume-type phase transitions on countable Markov shifts. Nonlinearity 34(7) (2021), 4819.CrossRefGoogle Scholar
Bissacot, R. and Freire, R.. On the existence of maximizing measures for irreducible countable Markov shifts: a dynamical proof. Ergod. Th. & Dynam. Sys. 34(4) (2014), 1103–1115.CrossRefGoogle Scholar
Bissacot, R., Mengue, J. and Pérez, E.. A large deviation principle for Gibbs states on Markov shifts at zero temperature. Preprint, 2016, arXiv:1612.05831.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Cham, 1975.CrossRefGoogle Scholar
Brémont, J.. Gibbs measures at temperature zero. Nonlinearity 16(2) (2003), 419–426.CrossRefGoogle Scholar
Buzzi, J. and Sarig, O.. Uniqueness of equilibrium measures for countable Markov shifts and multidimensional piecewise expanding maps. Ergod. Th. & Dynam. Sys. 23(5) (2003), 1383–1400.CrossRefGoogle Scholar
Chazottes, J.-R., Gambaudo, J.-M. and Ugalde, E.. Zero-temperature limit of one-dimensional Gibbs states via renormalization: the case of locally constant potentials. Ergod. Th. & Dynam. Sys. 31(4) (2011), 1109–1161.CrossRefGoogle Scholar
Chazottes, J.-R. and Hochman, M.. On the zero-temperature limit of Gibbs states. Commun. Math. Phys. 297(1) (2010), 265–281.CrossRefGoogle Scholar
Coelho-Filho, Z.. Entropy and ergodicity of skew-products over subshifts of finite type and central limit asymptotics. PhD Thesis, University of Warwick, 1990.Google Scholar
Cyr, V.. Countable Markov shifts with transient potentials. Proc. Lond. Math. Soc. (3) 103 (2011), 923–949.CrossRefGoogle Scholar
Freire, R. and Vargas, V.. Equilibrium states and zero temperature limit on topologically transitive countable Markov shifts. Trans. Amer. Math. Soc. 370(12) (2018), 8451–8465.CrossRefGoogle Scholar
Gurevich, B. M.. A variational characterization of one-dimensional countable state Gibbs random fields. Z. Wahrscheinlichkeitstheor. Verw. Geb. 68 (1984), 205–242.CrossRefGoogle Scholar
Iommi, G.. Ergodic optimization for renewal type shifts. Monatsh. Math. 150(2) (2007), 91–95.CrossRefGoogle Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Zero temperature limits of Gibbs-equilibrium states for countable alphabet subshifts of finite type. J. Stat. Phys. 119(3–4) (2005), 765–776.CrossRefGoogle Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Ergodic optimization for countable alphabet subshifts of finite type. Ergod. Th. & Dynam. Sys. 26(6) (2006), 1791–1803.CrossRefGoogle Scholar
Kempton, T.. Zero temperature limits of Gibbs equilibrium states for countable Markov shifts. J. Stat. Phys. 143(4) (2011), 795–806.CrossRefGoogle Scholar
Leplaideur, R.. A dynamical proof for the convergence of Gibbs measures at temperature zero. Nonlinearity 18(6) (2005), 2847–2880.CrossRefGoogle Scholar
Lopes, A. O. and Vargas, V.. Entropy, pressure, ground states and calibrated sub-actions for linear dynamics. Bull. Braz. Math. Soc. (N.S.) 53 (2022), 1073–1106.CrossRefGoogle Scholar
Mauldin, R. D. and Urbański, M.. Gibbs states on the symbolic space over an infinite alphabet. Israel J. Math. 125 (2001), 93–130.CrossRefGoogle Scholar
Morris, I. D.. Entropy for zero-temperature limits of Gibbs-equilibrium states for countable-alphabet subshifts of finite type. J. Stat. Phys. 126(2) (2007), 315–324.CrossRefGoogle Scholar
Ruelle, D.. Statistical mechanics of a one-dimensional lattice gas. Comm. Math. Phys. 9 (1968), 267–278.CrossRefGoogle Scholar
Sarig, O.. Lecture Notes on Thermodynamic Formalism for Topological Markov Shifts. Penn State, 2009. Available at: https://www.weizmann.ac.il/math/sarigo/lecture-notes.Google Scholar
Sarig, O. M.. Thermodynamic formalism for countable Markov shifts. Ergod. Th. & Dynam. Sys. 19(6) (1999), 1565–1593.CrossRefGoogle Scholar
Sarig, O. M.. Phase transitions for countable Markov shifts. Comm. Math. Phys. 217(3) (2001), 555–577.CrossRefGoogle Scholar
Shwartz, O.. Thermodynamic formalism for transient potential functions. Comm. Math. Phys. 366(2) (2019), 737–779.CrossRefGoogle Scholar
Souza, R. R. and Vargas, V.. Existence of Gibbs states and maximizing measures on a general one-dimensional lattice system with Markovian structure. Qual. Theory Dyn. Syst. 21(1) (2022), 5.CrossRefGoogle Scholar
van Enter, A. C. D. and Ruszel, W. M.. Chaotic temperature dependence at zero temperature. J. Stat. Phys. 127(3) (2007), 567–573.CrossRefGoogle Scholar