Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Conley, Clinton T.
Kechris, Alexander S.
and
Miller, Benjamin D.
2013.
Stationary probability measures and topological realizations.
Israel Journal of Mathematics,
Vol. 198,
Issue. 1,
p.
333.
Conley, Clinton
and
Miller, Benjamin
2017.
Measure reducibility of countable Borel equivalence relations.
Annals of Mathematics,
Vol. 185,
Issue. 2,
MILLER, BENJAMIN D.
2020.
On the existence of cocycle-invariant Borel probability measures.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 11,
p.
3150.
INSELMANN, MANUEL J.
and
MILLER, BENJAMIN D.
2021.
RECURRENCE AND THE EXISTENCE OF INVARIANT MEASURES.
The Journal of Symbolic Logic,
Vol. 86,
Issue. 1,
p.
60.
LOPES, ARTUR O.
and
MENGUE, JAIRO K.
2021.
Thermodynamic formalism for Haar systems in noncommutative integration: transverse functions and entropy of transverse measures.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 6,
p.
1835.
de Castro, G. G.
Lopes, Artur O.
and
Mantovani, G.
2021.
Modeling, Dynamics, Optimization and Bioeconomics IV.
Vol. 365,
Issue. ,
p.
79.
Tserunyan, Anush
2022.
Pointwise ergodic theorem for locally countable quasi-pmp graphs.
Journal of Modern Dynamics,
Vol. 18,
Issue. 0,
p.
609.


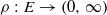 , we characterize the circumstances under which there is a probability measure
, we characterize the circumstances under which there is a probability measure 