We study the continuity of topological entropy of general diffeomorphisms on line. First, we prove that the entropy map is continuous with respect to the strong 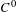$C^{0}$-topology on the union of uniformly topologically hyperbolic diffeomorphisms contained in 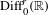$\text{Diff}_{0}^{r}(\mathbb{R})$ (whose first derivative is uniformly away from zero), which is a 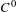$C^{0}$-open and 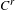$C^{r}$-dense subset of 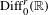$\text{Diff}_{0}^{r}(\mathbb{R})$, 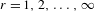$r=1,2,\ldots ,\infty$, and $\unicode[STIX]{x1D714}$ (real analytic). Second, we give some examples where entropy map is not continuous. Finally, we prove some results on the continuity of entropy of general diffeomorphisms on the (real) line.