Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T14:33:18.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy dimension for deterministic walks in random sceneries

Part of: Measure-theoretic ergodic theory Ergodic theory

Published online by Cambridge University Press:  29 April 2021

DOU DOU  and
KYEWON KOH PARK
DOU DOU*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing, Jiangsu210093, P.R. China
KYEWON KOH PARK
Affiliation:
Center for Mathematical Challenges, Korea Institute for Advanced Study, Seoul130-722, Korea (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Entropy dimension is an entropy-type quantity which takes values in 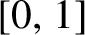$[0,1]$ and classifies different levels of intermediate growth rate of complexity for dynamical systems. In this paper, we consider the complexity of skew products of irrational rotations with Bernoulli systems, which can be viewed as deterministic walks in random sceneries, and show that this class of models can have any given entropy dimension by choosing suitable rotations for the base system.

Keywords

complexitydeterministic walkentropy dimensionsub-exponential growth

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification
Secondary: 37A05: Measure-preserving transformations 28D20: Entropy and other invariants
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 6 , June 2022 , pp. 1908 - 1925
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. Relative complexity of random walks in random sceneries. Ann. Probab. 40(6) (2012), 2460–2482.10.1214/11-AOP688CrossRefGoogle Scholar
Aaronson, J. and Keane, M.. The visits to zero of some deterministic random walks. Proc. Lond. Math. Soc. 44 (1982), 535–553.10.1112/plms/s3-44.3.535CrossRefGoogle Scholar
Ahn, Y., Dou, D. and Park, K. K.. Entropy dimension and its variational principle. Studia Math. 199(3) (2010), 295–309.10.4064/sm199-3-6CrossRefGoogle Scholar
Avila, A., Dolgopyat, D., Duryev, E. and Sarig, O.. The visits to zero of a random walk driven by an irrational rotation. Israel J. Math. 207 (2015), 653–717.CrossRefGoogle Scholar
Blanchard, F.. A disjointness theorem involving topological entropy. Bull. Soc. Math. France 121 (1993), 465–478.10.24033/bsmf.2216CrossRefGoogle Scholar
Cassaigne, J.. Constructing infinite words of intermediate complexity. Developments in Language Theory (Lecture Notes in Computer Science, 2450). Springer, Berlin, 2003, pp. 173–184.CrossRefGoogle Scholar
De Carvalho, M.. Entropy dimension of dynamical systems. Portugal. Math. 54(1) (1997), 19–40.Google Scholar
Conze, J.-P. and Keane, M.. Ergodicité dun flot cylindrique. Séminaire de Probabilités, I (Université de Rennes, Rennes, 1976). Département de Mathématiques et Informatique, Université de Rennes, Rennes, 1976, Exp. No. 5.Google Scholar
Dou, D., Huang, W. and Park, K. K.. Entropy dimension of topological dynamics. Trans. Amer. Math. Soc. 363 (2011), 659–680.CrossRefGoogle Scholar
Dou, D., Huang, W. and Park, K. K.. Entropy dimension of measure preserving systems. Trans. Amer. Math. Soc. 371 (2019), 7029–7065.CrossRefGoogle Scholar
Dou, D. and Park, K. K.. Examples of entropy generating sequence. Sci. China Math. 54(3) (2011), 531–538.CrossRefGoogle Scholar
Ferenczi, S. and Park, K. K.. Entropy dimensions and a class of constructive examples. Discrete Contin. Dyn. Syst. 17(1) (2007), 133–141.CrossRefGoogle Scholar
Hochman, M.. Slow entropy and differentiable models for infinite-measure preserving ${\mathbb{Z}}^k$ actions. Ergod. Th. & Dynam. Sys. 32(2) (2012), 653–674.10.1017/S0143385711000782CrossRefGoogle Scholar
Jung, U., Lee, J. and Park, K. K.. Constructions of subshifts with positive topological entropy dimension. Preprint, 2016, arXiv:1601.07259v1.Google Scholar
Jung, U., Lee, J. and Park, K. K.. Topological entropy dimension and directional entropy dimension for ${\mathbb{Z}}^2$ -subshifts. Entropy 19 (2017), Paper No. 46, 13 pp.10.3390/e19020046CrossRefGoogle Scholar
Katok, A. and Thouvenot, J.-P.. Slow entropy type invariants and smooth realization of commuting measure-preserving transformations. Ann. Inst. Henri Poincaré Probab. Stat. 33(3) (1997), 323–338.10.1016/S0246-0203(97)80094-5CrossRefGoogle Scholar
Khinchin, A. Y.. Continued Fractions. Noordhoff, Groningen, 1963.Google Scholar
Kim, H. and Park, S.. Toeplitz sequences of intermediate complexity. J. Korean Math. Soc. 48(2) (2011), 383–395.10.4134/JKMS.2011.48.2.383CrossRefGoogle Scholar
Park, K. K.. On directional entropy functions. Israel J. Math. 113 (1999), 243–267.10.1007/BF02780179CrossRefGoogle Scholar
Park, K. K.. A counterexample of the entropy of a skew product. Indag. Math. 9(4) (1998), 537–548.CrossRefGoogle Scholar
de Vries, J.. Elements of Topological Dynamics. Kluwer, Dordrecht, 1993.CrossRefGoogle Scholar