Article contents
The dynamical zeta function for commuting automorphisms of zero-dimensional groups
Published online by Cambridge University Press: 08 November 2016
Abstract
For a 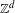 $\mathbb{Z}^{d}$-action
$\mathbb{Z}^{d}$-action  $\unicode[STIX]{x1D6FC}$ by commuting homeomorphisms of a compact metric space, Lind introduced a dynamical zeta function that generalizes the dynamical zeta function of a single transformation. In this article, we investigate this function when
$\unicode[STIX]{x1D6FC}$ by commuting homeomorphisms of a compact metric space, Lind introduced a dynamical zeta function that generalizes the dynamical zeta function of a single transformation. In this article, we investigate this function when  $\unicode[STIX]{x1D6FC}$ is generated by continuous automorphisms of a compact abelian zero-dimensional group. We address Lind’s conjecture concerning the existence of a natural boundary for the zeta function and prove this for two significant classes of actions, including both zero entropy and positive entropy examples. The finer structure of the periodic point counting function is also examined and, in the zero entropy case, we show how this may be severely restricted for subgroups of prime index in
$\unicode[STIX]{x1D6FC}$ is generated by continuous automorphisms of a compact abelian zero-dimensional group. We address Lind’s conjecture concerning the existence of a natural boundary for the zeta function and prove this for two significant classes of actions, including both zero entropy and positive entropy examples. The finer structure of the periodic point counting function is also examined and, in the zero entropy case, we show how this may be severely restricted for subgroups of prime index in 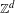 $\mathbb{Z}^{d}$. We also consider a related open problem concerning the appearance of a natural boundary for the dynamical zeta function of a single automorphism, giving further weight to the Pólya–Carlson dichotomy proposed by Bell and the authors.
$\mathbb{Z}^{d}$. We also consider a related open problem concerning the appearance of a natural boundary for the dynamical zeta function of a single automorphism, giving further weight to the Pólya–Carlson dichotomy proposed by Bell and the authors.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 2
- Cited by


