Article contents
Discontinuity of Lyapunov exponents near fiber bunched cocycles
Published online by Cambridge University Press: 19 September 2016
Abstract
We give examples of locally constant 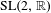 $\text{SL}(2,\mathbb{R})$-cocycles over a Bernoulli shift that are discontinuity points for Lyapunov exponents in the Hölder topology and are arbitrarily close to satisfying the fiber bunching inequality. Backes, Brown, and the author [Continuity of Lyapunov exponents for cocycles with invariant holonomies. Preprint, 2015, arXiv:1507.08978] have shown that the Lyapunov exponents vary continuously when restricted to the space of fiber bunched Hölder continuous cocycles. Our examples give evidence that this theorem is optimal within certain families of Hölder cocycles.
$\text{SL}(2,\mathbb{R})$-cocycles over a Bernoulli shift that are discontinuity points for Lyapunov exponents in the Hölder topology and are arbitrarily close to satisfying the fiber bunching inequality. Backes, Brown, and the author [Continuity of Lyapunov exponents for cocycles with invariant holonomies. Preprint, 2015, arXiv:1507.08978] have shown that the Lyapunov exponents vary continuously when restricted to the space of fiber bunched Hölder continuous cocycles. Our examples give evidence that this theorem is optimal within certain families of Hölder cocycles.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 6
- Cited by


