Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:02:17.394Z Has data issue: false hasContentIssue false
  • English
  • Français

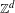Directional dynamical cubes for minimal $\mathbb{Z}^{d}$-systems

Part of: Topological dynamics Connections with other structures, applications

Published online by Cambridge University Press:  26 June 2019

CHRISTOPHER CABEZAS Open the ORCID record for CHRISTOPHER CABEZAS [Opens in a new window] ,
SEBASTIÁN DONOSO Open the ORCID record for SEBASTIÁN DONOSO [Opens in a new window]  and
ALEJANDRO MAASS Open the ORCID record for ALEJANDRO MAASS [Opens in a new window]
CHRISTOPHER CABEZAS
Affiliation:
Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático, Universidad de Chile & UMI-CNRS 2807, Av. Beauchef 851, Santiago, Chile email [email protected], [email protected]
SEBASTIÁN DONOSO
Affiliation:
Instituto de Ciencias de la Ingeniería, Universidad de O’Higgins, Av. Lib. Bernardo O’Higgins 611, Rancagua, Chile email [email protected]
ALEJANDRO MAASS
Affiliation:
Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático, Universidad de Chile & UMI-CNRS 2807, Av. Beauchef 851, Santiago, Chile email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notions of directional dynamical cubes and directional regionally proximal relation defined via these cubes for a minimal 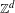$\mathbb{Z}^{d}$-system 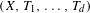$(X,T_{1},\ldots ,T_{d})$. We study the structural properties of systems that satisfy the so-called unique closing parallelepiped property and we characterize them in several ways. In the distal case, we build the maximal factor of a 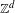$\mathbb{Z}^{d}$-system 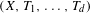$(X,T_{1},\ldots ,T_{d})$ that satisfies this property by taking the quotient with respect to the directional regionally proximal relation. Finally, we completely describe distal 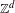$\mathbb{Z}^{d}$-systems that enjoy the unique closing parallelepiped property and provide explicit examples.

Keywords

topological dynamicsminimal systemscubespacesdirectional cubescommuting transformations

MSC classification

Primary: 54H20: Topological dynamics
Secondary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 12 , December 2020 , pp. 3257 - 3295
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antolín Camarena, O. and Szegedy, B.. Nilspaces, nilmanifolds and their morphisms. Preprint, 2010,arXiv:1009.3825.Google Scholar
Auslander, J.. Minimal flows and their extensions. Notas de Matemática [Mathematical Notes], Volume 122 (North-Holland Mathematics Studies, 153). North-Holland, Amsterdam, 1988.Google Scholar
Austin, T.. On the norm convergence of non-conventional ergodic averages. Ergod. Th. & Dynam. Sys. 30(2) (2010), 321–338.Google Scholar
Austin, T.. Multiple recurrence and the structure of probability-preserving systems. PhD Thesis, University of California, Los Angeles, 2010.Google Scholar
Cabezas, C.. Cubos dinámicos direccionales para $\mathbb{Z}^{d}$-sistemas minimales. Master’s Thesis, Universidad de Chile, 2018.Google Scholar
Candela, P.. Notes on nilspaces: algebraic aspects. Discrete Anal. (2017), Paper No. 15.Google Scholar
Candela, P.. Notes on compact nilspaces. Discrete Anal. (2017), Paper No. 16.Google Scholar
Donoso, S. and Sun, W.. Dynamical cubes and a criteria for systems having product extensions. J. Mod. Dyn. 9 (2015), 365–405.Google Scholar
Donoso, S. and Sun, W.. A pointwise cubic average for two commuting transformations. Israel J. Math. 216(2) (2016), 657–678.Google Scholar
Donoso, S. and Sun, W.. Pointwise multiple averages for systems with two commuting transformations. Ergod. Th. & Dynam. Sys. 38(6) (2018), 2132–2157.Google Scholar
Donoso, S. and Sun, W.. Pointwise convergence of some multiple ergodic averages. Adv. Math. 330 (2018), 946–996.Google Scholar
Glasner, E.. Topological ergodic decompositions and applications to products of powers of a minimal transformation. J. Anal. Math. 64 (1994), 241–262.Google Scholar
Glasner, E., Gutman, Y. and Ye, X.. Higher order regionally proximal equivalence relations for general minimal group actions. Adv. Math. 333 (2018), 1004–1041.Google Scholar
Gutman, Y., Manners, F. and Varjú, P.. The structure theory of nilspaces III: Inverse limit representations and topological dynamics. Preprint, 2016, arXiv:1605.08950.Google Scholar
Gutman, Y., Manners, F. and Varjú, P.. The structure theory of nilspaces I. J. Anal. Math. (2018), in press.Google Scholar
Gutman, Y., Manners, F. and Varjú, P.. The structure theory of nilspaces II: Representation as nilmanifolds. Trans. Amer. Math. Soc. 371 (2019), 4951–4992.Google Scholar
Host, B.. Ergodic seminorms for commuting transformations and applications. Studia Math. 195(1) (2009), 31–49.Google Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.Google Scholar
Host, B., Kra, B. and Maass, A.. Nilsequences and a structure theorem for topological dynamical systems. Adv. Math. 224(1) (2010), 103–129.Google Scholar
Huang, W., Shao, S. and Ye, X.. Nil Bohr-sets and almost automorphy of higher order. Mem. Amer. Math. Soc. 241(1143) (2016).Google Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequences of translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25(1) (2005), 201–213.Google Scholar
Parry, W.. Ergodic properties of affine transformations and flows on nilmanifolds. Amer. J. Math. 91 (1969), 757–771.Google Scholar
Shao, S. and Ye, X.. Regionally proximal relation of order d is an equivalence one for minimal systems and a combinatorial consequence. Adv. Math. 231(3–4) (2012), 1786–1817.Google Scholar
Tao, T.. Norm convergence of multiple ergodic averages for commuting transformations. Ergod. Th. & Dynam. Sys. 28(2) (2008), 657–688.Google Scholar
Tu, S. and Ye, X.. Dynamical parallelepipeds in minimal systems. J. Dynam. Differential Equations 25(3) (2013), 765–776.Google Scholar