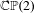Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T15:50:23.095Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimension of ergodic measures and currents on $\mathbb{C}\mathbb{P}(2)$

Part of: Complex dynamical systems Smooth dynamical systems: general theory Holomorphic mappings and correspondences Pluripotential theory

Published online by Cambridge University Press:  04 January 2019

CHRISTOPHE DUPONT  and
AXEL ROGUE
CHRISTOPHE DUPONT
Affiliation:
Univ Rennes, CNRS, IRMAR – UMR 6625, F-35000 Rennes, France email [email protected], [email protected]
AXEL ROGUE
Affiliation:
Univ Rennes, CNRS, IRMAR – UMR 6625, F-35000 Rennes, France email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 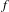$f$ be a holomorphic endomorphism of 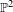$\mathbb{P}^{2}$ of degree 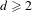$d\geq 2$. We estimate the local directional dimensions of closed positive currents $S$ with respect to ergodic dilating measures $\unicode[STIX]{x1D708}$. We infer several applications. The first one is an upper bound for the lower pointwise dimension of the equilibrium measure, towards a Binder–DeMarco’s formula for this dimension. The second one shows that every current $S$ containing a measure of entropy 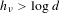$h_{\unicode[STIX]{x1D708}}>\log d$ has a directional dimension 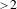${>}2$, which answers a question of de Thélin–Vigny in a directional way. The last one estimates the dimensions of the Green current of Dujardin’s semi-extremal endomorphisms.

Keywords

dimension theoryLyapunov exponentsnormal forms

MSC classification

Primary: 37C45: Dimension theory of dynamical systems 37F10: Polynomials; rational maps; entire and meromorphic functions 32H50: Iteration problems
Secondary: 32U40: Currents
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 8 , August 2020 , pp. 2131 - 2155
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berteloot, F. and Dupont, C.. Une caractérisation des endomorphismes de Lattès par leur mesure de Green. Comment. Math. Helv. 80(2) (2005), 433–454.CrossRefGoogle Scholar
Berteloot, F., Dupont, C. and Molino, L.. Normalization of bundle holomorphic contractions and applications to dynamics. Ann. Inst. Fourier (Grenoble) 58(6) (2008), 2137–2168.10.5802/aif.2409CrossRefGoogle Scholar
Berteloot, F. and Loeb, J.-J.. Spherical hypersurfaces and Lattès rational maps. J. Math. Pures Appl. (9) 77(7) (1998), 655–666.CrossRefGoogle Scholar
Berteloot, F. and Loeb, J.-J.. Une caractérisation géométrique des exemples de Lattès de ℙk. Bull. Soc. Math. France 129(2) (2001), 175–188.CrossRefGoogle Scholar
Binder, I. and DeMarco, L.. Dimension of pluriharmonic measure and polynomial endomorphisms of ℂn. Int. Math. Res. Not. IMRN 2003 (2003), 613–625.CrossRefGoogle Scholar
Briend, J.-Y.. Exposants de Liapounoff et points périodiques d’endomorphismes holomorphes de CP(k). PhD Thesis, Université Paul Sabatier de Toulouse, 1997.CrossRefGoogle Scholar
Briend, J.-Y. and Duval, J.. Exposants de Liapounoff et distribution des points périodiques d’un endomorphisme de CPk. Acta Math. 182(2) (1999), 143–157.CrossRefGoogle Scholar
Briend, J.-Y. and Duval, J.. Deux caractérisations de la mesure d’équilibre d’un endomorphisme de Pk(C). Publ. Math. Inst. Hautes Études Sci. 2001(93) (2001), 145–159.10.1007/s10240-001-8190-4CrossRefGoogle Scholar
Brin, M. and Katok, A.. On local entropy. Geometric Dynamics (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 30–38.CrossRefGoogle Scholar
de Thélin, H.. Un phénomène de concentration de genre. Math. Ann. 332(3) (2005), 483–498.Google Scholar
de Thélin, H.. Sur les exposants de Lyapounov des applications méromorphes. Invent. Math. 172(1) (2008), 89–116.CrossRefGoogle Scholar
de Thélin, H.. Minoration de la dimension de Hausdorff du courant de Green. Preprint, 2017, arXiv:1709. 01356.Google Scholar
de Thélin, H. and Vigny, G.. On the measures of large entropy on a positive closed current. Math. Z. 280(3–4) (2015), 919–944.CrossRefGoogle Scholar
Demailly, J.-P.. Complex Analytic and Differential Geometry, 2012, available at https://www-fourier.ujf-grenoble.fr/∼demailly/manuscripts/agbook.pdf.Google Scholar
Dinh, T.-C.. Sur les applications de Lattès de ℙk. J. Math. Pures Appl. (9) 80(6) (2001), 577–592.CrossRefGoogle Scholar
Dinh, T.-C.. Attracting current and equilibrium measure for attractors on ℙk. J. Geom. Anal. 17(2) (2007), 227–244.10.1007/BF02930722CrossRefGoogle Scholar
Dinh, T.-C. and Dupont, C.. Dimension de la mesure d’équilibre d’applications méromorphes. J. Geom. Anal. 14(4) (2004), 613–627.10.1007/BF02922172CrossRefGoogle Scholar
Dinh, T.-C. and Sibony, N.. Dynamics in Several Complex Variables: Endomorphisms of Projective Spaces and Polynomial-like Mappings (Lecture Notes in Mathematics, 1998). Springer, Berlin, 2010, pp. 165–294.Google Scholar
Dujardin, R.. Fatou directions along the Julia set for endomorphisms of ℂℙk. J. Math. Pures Appl. (9) 98(6) (2012), 591–615.CrossRefGoogle Scholar
Dupont, C.. On the dimension of invariant measures of endomorphisms of ℂℙ(k). Math. Ann. 349(3) (2011), 509–528.CrossRefGoogle Scholar
Dupont, C.. Large entropy measures for endomorphisms of ℂℙk. Israel J. Math. 192(2) (2012), 505–533.CrossRefGoogle Scholar
Dupont, C. and Taflin, J.. Dynamics of fibered endomorphisms of $\mathbb{P}^{k}$. Preprint, 2018, arXiv:1811.06909.Google Scholar
Fornaess, J. E. and Sibony, N.. Some open problems in higher dimensional complex analysis and complex dynamics. Publ. Mat. 45(2) (2001), 529–547.CrossRefGoogle Scholar
Jonsson, M. and Varolin, D.. Stable manifolds of holomorphic diffeomorphisms. Invent. Math. 149(2) (2002), 409–430.CrossRefGoogle Scholar
Mañé, R.. The Hausdorff dimension of invariant probabilities of rational maps. Dynamical systems, Valparaiso 1986 (Lecture Notes in Mathematics, 1331). Springer, Berlin, 1988, pp. 86–117.10.1007/BFb0083068CrossRefGoogle Scholar
Pesin, Y. B.. Dimension Theory in Dynamical Systems (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 1997, contemporary views and applications.CrossRefGoogle Scholar
Sibony, N.. Dynamique des applications rationnelles de Pk. Dynamique et géométrie Complexes (Lyon, 1997) (Panor. Synthèses, 8). Société Mathématique de France, Paris, 1999, ix–x, xi–xii, 97–185.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.CrossRefGoogle Scholar
Young, L.-S.. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2(1) (1982), 109–124.CrossRefGoogle Scholar