Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nawata, Norio
2012.
Fundamental group of uniquely ergodic Cantor minimal systems.
Advances in Mathematics,
Vol. 230,
Issue. 2,
p.
746.


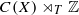 associated with (
associated with (