Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T09:17:19.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Decompositions and measures on countable Borel equivalence relations

Part of: Ergodic theory Set theory

Published online by Cambridge University Press:  04 December 2020

RUIYUAN CHEN
RUIYUAN CHEN*
Affiliation:
Department of Mathematics, University of Illinois at Urbana–Champaign, Urbana, IL61801, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the uniform measure-theoretic ergodic decomposition of a countable Borel equivalence relation 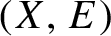$(X, E)$ may be realized as the topological ergodic decomposition of a continuous action of a countable group $\Gamma \curvearrowright X$ generating E. We then apply this to the study of the cardinal algebra 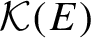$\mathcal {K}(E)$ of equidecomposition types of Borel sets with respect to a compressible countable Borel equivalence relation 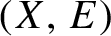$(X, E)$ . We also make some general observations regarding quotient topologies on topological ergodic decompositions, with an application to weak equivalence of measure-preserving actions.

Keywords

cardinal algebrascountable Borel equivalence relationsergodic decomposition

MSC classification

Primary: 03E15: Descriptive set theory 37A20: Orbit equivalence, cocycles, ergodic equivalence relations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 12 , December 2021 , pp. 3671 - 3703
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abért, M. and Elek, G.. The space of actions, partition metric and combinatorial rigidity. Preprint, 2011, arXiv:1108.2147.Google Scholar
Becker, H. and Kechris, A. S.. The Descriptive Set Theory of Polish Group Actions (London Mathematical Society Lecture Note Series, 232). Cambridge University Press, Cambridge, 1996.CrossRefGoogle Scholar
Burton, P. J. and Kechris, A. S.. Weak containment of measure preserving group actions. Ergod. Th. & Dynam. Sys. 40(10) (2020), 2681–2733.10.1017/etds.2019.26CrossRefGoogle Scholar
Chen, R.. Notes on quasi-Polish spaces. Preprint, 2018, arXiv:1809.07440.Google Scholar
Chuaqui, R. B.. Cardinal algebras and measures invariant under equivalence relations. Trans. Amer. Math. Soc. 142 (1969), 61–79.Google Scholar
de Brecht, M.. Quasi-Polish spaces. Ann. Pure Appl. Logic 164(3) (2013), 356–381.CrossRefGoogle Scholar
Dougherty, R., Jackson, S. and Kechris, A. S.. The structure of hyperfinite Borel equivalence relations. Trans. Amer. Math. Soc. 341(1) (1994), 193–225.CrossRefGoogle Scholar
Gierz, G., Hofmann, K. H., Keimel, K., Lawson, J. D., Mislove, M. and Scott, D. S.. Continuous Lattices and Domains (Encyclopedia of Mathematics and Its Applications, 93). Cambridge University Press, Cambridge, 2003.CrossRefGoogle Scholar
Heckmann, R.. Spatiality of countably presentable locales (proved with the Baire category theorem). Math. Structures Comput. Sci. 25(7) (2015), 1607–1625.CrossRefGoogle Scholar
Kechris, A. S.. Classical Descriptive Set Theory (Graduate Texts in Mathematics, 156). Springer, New York, 1995.CrossRefGoogle Scholar
Kechris, A. S.. Global Aspects of Ergodic Group Actions. American Mathematical Society, Providence, RI, 2010.10.1090/surv/160CrossRefGoogle Scholar
Kechris, A. S. and Macdonald, H. L.. Borel equivalence relations and cardinal algebras. Fund. Math. 235 (2016), 183–198.Google Scholar
Kechris, A. S. and Miller, B. D.. Topics in Orbit Equivalence (Lecture Notes in Mathematics, 1852). Springer, Berlin, 2004.CrossRefGoogle Scholar
Miller, D. E.. A selector for equivalence relations with ${G}_{\delta }$ orbits. Proc. Amer. Math. Soc. 72(2) (1978), 365–369.Google Scholar
Nadkarni, M. G.. On the existence of a finite invariant measure. Proc. Indian Acad. Sci. Math. Sci. 100(3) (1990), 203–220.CrossRefGoogle Scholar
Tarski, A.. Cardinal Algebras. Oxford University Press, New York, 1949.Google Scholar